
ハルビン工業大学(深圳)• 2024 • コンピュータ・アーキテクチャ Lab Guidebook 2024・日本語訳版
HITSZ 计算机体系结构实验指导书 2024
当サイト内のコンテンツの無断転載、引用、コピーは禁止されています。
コース概要
本GuideBookは、ハルビン工業大学(深圳)「コンピュータアーキテクチャ」のLab指導資料です。PCでページ左側に各小節の目次、索引が表示されます。
必ず順番に指導書を読み進め、疑問点があれば積極的に質問してください。
注意事項
このコース資料は、ハルビン工業大学(深圳)「コンピュータアーキテクチャ(実験)」2024年秋学期の授業に限り使用可能です。
資料の無断転載や他の用途での使用を固く禁じます。
内容の構成
本コース実験の目的は、受講者がコンピュータアーキテクチャにおける キャッシュ最適化、命令レベルの最適化、および並列最適化 を習得することにあります。具体的には、以下の内容を含みます:
- 基本的な実験フレームワークの作成
- アセンブリコードを使用して行列積とLlama推論フレームワークを実装。
- Llama推論フレームワークにおける行列積(または行列-ベクトル積)が推論時間に占める割合を分析。
- キャッシュ最適化アセンブリプログラムの作成
- プロセッサアーキテクチャのキャッシュ階層とサイズを理解。
- 行列積におけるデータの読み書きがキャッシュに与える影響を把握。
- データとキャッシュの特性に基づき、データの読み書き方法を最適化し、キャッシュの利用率を向上させ、行列積の性能を改善。
- 命令レベル並列化CPUプログラムの作成
- 命令レベル並列化による行列積の高速化を理解。
- CUDAプログラミング
- 基本的なGPU行列積プログラムの作成。
- 共有メモリを使用した最適化。
- Llama.cプログラムの高速化
- 自主探索テーマとして提供
Labs一覧
以下の内容を6つのLabsに分割して進行します。
| テーマ | Lab | 実験時間 |
|---|---|---|
| CPU最適化 | 実験1:行列積の作成 | 4時間 |
| 実験2:キャッシュを最適化した行列積の作成 | 4時間 | |
| 実験3:命令レベル並列化、ベクトル命令、並列最適化を使用した行列積作成 | 8時間 | |
| 📝 実験レポート作成 | ||
| GPU最適化 | 実験4:C/CUDAを使用したGPUコード作成 | 4時間 |
| 実験5:共有メモリを用いたGPUコードの最適化 | 4時間 | |
| 📝 実験レポート作成 | ||
| Llama最適化 | 実験6:Llamaモデル推論性能の評価 | 4時間 |
| 📝 実験レポート作成 | ||
授業スケジュール
授業は、以下の3つのクラスに分かれて行われます。授業はすべてT2210で実施されます。
特定の週限で他の授業や試験などが重複する場合は、以下のスケジュールを参照してご自由に他のクラスで行うことが可能です。
| 週次 | 授業内容 | Aクラス | Bクラス | Cクラス |
|---|---|---|---|---|
| 11週目 | 実験1 | 水曜 9-12限 | 木曜 9-12限 | 土曜 5-8限 |
| 12週目 | 実験2 | 水曜 9-12限 | 木曜 9-12限 | 金曜 9-12限 |
| 13週目 | 実験3-1 | 水曜 9-12限 | 金曜 5-8限 | 土曜 5-8限 |
| 14週目 | 実験3-2 | 木曜 1-4限 | 木曜 9-12限 | 金曜 9-12限 |
| 15週目 | 実験4 | 木曜 1-4限 | 木曜 9-12限 | 金曜 9-12限 |
| 16週目-1 | 実験5 | 月曜 1-4限 | 木曜 1-4限 | 月曜 5-8限 |
| 16週目-2 | 実験6 | 水曜 1-4限 | 金曜 9-12限 | 木曜 9-12限 |
その他
1. 実験パッケージのダウンロード
キャンパスネットを利用したダウンロードリンクが提供されます。
2. Labの提出方法
1. ログイン
- 生徒用ログインURL:http://labgrader.hitsz.edu.cn:8000
- 推奨ブラウザはChromeです。初期のユーザー名とパスワードはどちらも学籍番号です。
初回ログイン後は、パスワードの変更をおすすめします。手順は下の「5. パスワード変更」を参照してください。
2. コースの確認
ログイン後、自分が登録しているコースを確認できます。
- コース名をクリックすると、コースの詳細が表示されます。
- 提出期限に特に注意してください。
3. 成果の提出
- 提出開始をクリックして課題の解答やファイルの提出を行います。
- File inputをクリックし、提出するファイルを選択します。
- ファイルを選択したら、画面右下の提出ボタンをクリックして提出を完了します。
- ページが遷移したら、提出成功を示すの場合、提出成功です。
※提出中にブラウザを閉じると失敗する可能性があるので注意してください。
4. 再提出
- 提出後でも提出期限内であれば、再提出が可能です。
5. パスワードの変更
- 画面右上のアカウント情報をクリックすると、パスワード変更画面に移動します。
6. 注意事項
- 提出期限内であれば、再提出が可能です(提出回数の制限はありません)。
- 提出期限後は提出不可となりますので注意してください。
- 提出時、ファイルの拡張子は各提出部分で指定された場合はそのファイル拡張子を持つファイルをアップロードしなさい。
- 256MBを超えるファイルの提出は現在対応していません。
3. 実験室のネットワークについて
T2210のUbuntuがインターネットに接続できない場合は、以下の設定を行ってください:
| 項目 | 設定値 |
|---|---|
| IP | 10.251.137.[コンピュータ番号] |
| サブネットマスク | 255.255.255.0 |
| ゲートウェイ | 10.251.137.254 |
| DNS | 10.248.98.30 |
Lab1 行列乗算
Lab目的
- コンピュータの命令セットアーキテクチャやアドレスモードの理解。
- 行列積プログラムを実装することで、x86-64アセンブリ言語のさまざまなアドレッシングモードを学び応用する。
- ハードウェアレベルでメモリにアクセスし操作する仕組みの理解。
Lab前の準備
- アセンブリ言語の基本概念を解明し、特に以下のアドレッシングモードを重点的に理解する:
- レジスタ間接アドレッシング
- ベース+インデックスアドレッシング
- 即値アドレッシング
- 比例インデックスアドレッシング
- Lab環境:x86アセンブラとデバッガがインストールされたLinuxコンピュータ。
Lab原理
分割行列積と乗算走査法
行列$A$が$M \times K$のサイズ、行列$B$が$K \times N$のサイズであるとする。このとき、行列$A$と行列$B$の積$C$は$M \times N$のサイズとなり、行列$C$の各要素は次の式で計算される:$$C_{ij} = \sum_{k=1}^{K} A_{ik} \cdot B_{kj}, \quad i=1,2,\dots,M; \, j=1,2,\dots,N$$
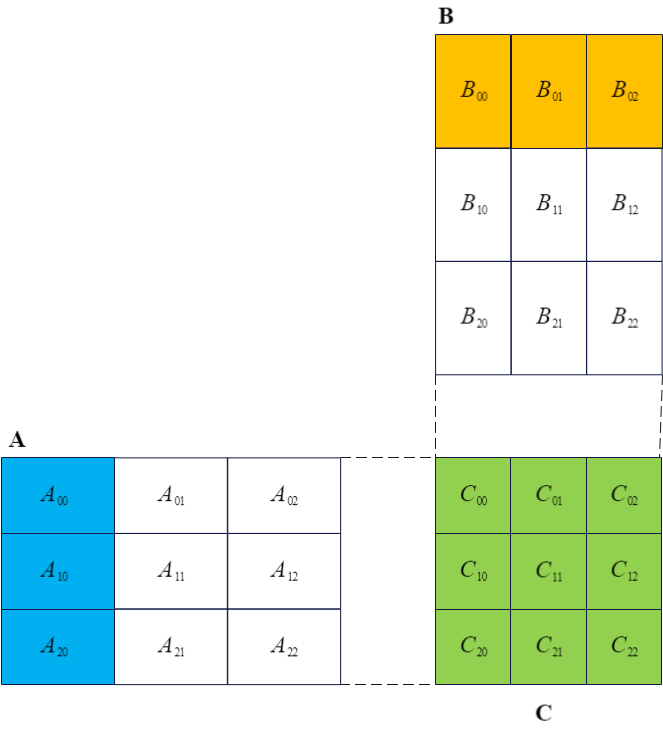
行列$A$、行列$B$、および行列$C$を分割行列積の定義に基づき図2-1のように分割する。定義より、次のように計算される:$$C_{00} = A_{00} \cdot B_{00} + A_{01} \cdot B_{10} + A_{02} \cdot B_{20}$$
この$C_{00}$を計算するには、行列$A$と行列$B$のすべての分割部分について、$K$次元に沿った計算を行う必要がある。
一般的に、結果行列の2次元を先に走査し、残りの1次元を最後に走査する方法がよく用いられる。たとえば、上記の行列$C$の各要素を計算する式は、典型的な ijk走査方式 である。この方式では、最後の次元を走査し終えた時点で、行列$C$の1つの要素の計算が完了するという利点がある。
一方、kij走査方式(またはランクK更新)もよく使用される。ijk走査方式とは異なり、kij走査方式では行列$C$の中間結果を保持する必要がある。図1-1に示されるように、行列$A$の1列と行列$B$の1行を走査するだけでは、行列$C$の各要素の一部の結果しか得られない。行列$A$と行列$B$のすべての分割部分を走査し終えた時点で、ようやく行列$C$の最終結果が得られる。kij走査方式は、空間アクセスの局所性をより確保し、キャッシュの利用効率を向上させる点で優れている。
x86-64概要
x86-64はx86の64ビット拡張版であり、高い互換性を保ちながら、レジスタと仮想アドレス空間を64ビットに拡張し、命令セットの機能と性能を向上させている。
x86-64アーキテクチャは、制御と状態レジスタ、プログラムポインタレジスタ、汎用レジスタ、ベクトルレジスタなど、さまざまなタイプのレジスタを備えている(表1-1参照)。
| 種類 | 名前 | ビット幅 | 説明 |
|---|---|---|---|
| 制御と状態レジスタ | RFLAGS | 64 | プロセッサのフラグ情報(例:ゼロフラグ(ZF)、符号ビット(SF)、キャリービット(CF)、オーバーフロービット(OF)、割り込み許可ビット(IF)など) |
| ポインタレジスタ | RIP | 64 | 現在の命令のアドレス |
| 汎用レジスタ | RAX | 64 | 累積用、積や被除数の下位64ビット、商の格納、またはサブルーチンの戻り値の格納に使用 |
| RBX | 64 | ベースレジスタとして使用 | |
| RCX | 64 | カウンタ、またはサブルーチン呼び出し時の第4引数を格納 | |
| RDX | 64 | データレジスタ、積や被除数の上位64ビット、余りの格納、またはサブルーチン呼び出し時の第3引数を格納 | |
| RSI | 64 | 文字列操作のソースインデックス、またはサブルーチン呼び出し時の第2引数 | |
| RDI | 64 | 文字列操作のデスティネーションインデックス、またはサブルーチン呼び出し時の第1引数 | |
| RSP | 64 | スタックポインタ | |
| RBP | 64 | スタックの基準ポインタ | |
| R8~R15 | 64 | 汎用(R8、R9はサブルーチン呼び出し時の第5、第6引数として使用) | |
| ベクトルレジスタ | XMM0~XMM15 | 128 | SSE(ストリーミングSIMD拡張)レジスタ;YMMの下位128ビット |
| YMM0~YMM15 | 256 | AVX(アドバンスドベクトル拡張)レジスタ |
x86-64アーキテクチャの一般的なアドレッシングモードには、即値アドレッシング、レジスタアドレッシング、直接アドレッシング、レジスタ間接アドレッシング、ベース変数アドレッシング、および比例インデックスアドレッシングが含まれる(表1-2参照)。
| アドレッシングモード | 使用例 | 説明 |
|---|---|---|
| 即値アドレッシング | mov $0x1234, %rax | RAX ← 0x1234 |
| レジスタアドレッシング | mov %r8, %rax | RAX ← R8 |
| 直接アドレッシング | mov 0x1234, %rax | RAX ← MEM[0x1234] |
| レジスタ間接アドレッシング | mov (%rsp), %rax | RAX ← MEM[RSP] |
| ベース変数アドレッシング | mov -20(%rsp), %rax | RAX ← MEM[RSP – 20] |
| 比例インデックスアドレッシング | mov -20(%rsp, %rcx, 4), %rax | RAX ← MEM[RSP – 20 + RCX*4] |
表1-2からわかるように、直接アドレッシング、レジスタ間接アドレッシング、およびベース変数アドレッシングは、いずれも比例インデックスアドレッシングの特殊なケースと見なせる。
x87 FPU
x87 FPU(浮動小数点演算ユニット)は、次のようなレジスタを備えている:
- 8個の80ビット汎用レジスタ(R0~R7)
- 3個の16ビット状態および制御レジスタ
- 2個の48ビットポインタレジスタ
- 1個の11ビットオペコードレジスタ
図1-2にこれを示す。
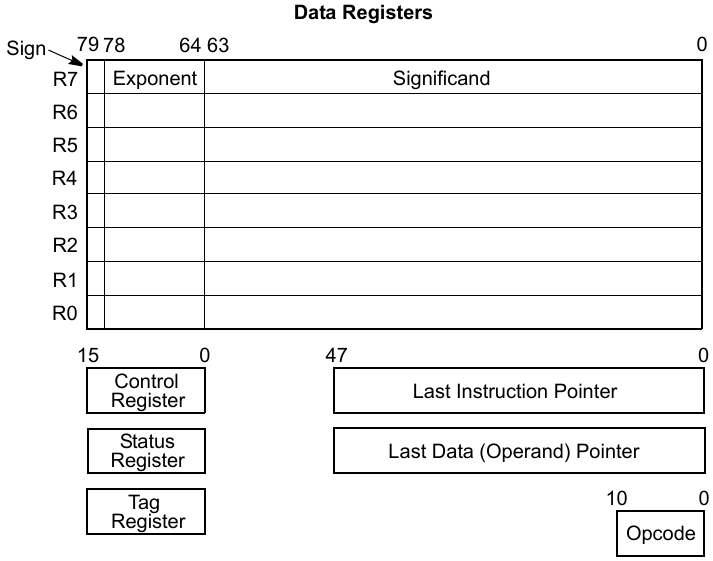
汎用レジスタは、計算データの格納に使用されます。データが汎用レジスタに書き込まれると、自動的に80ビットの拡張倍精度浮動小数点数(Double Extended-Precision Floating-Point)に変換されます。
一方、汎用レジスタからメモリにデータを書き込む際は、浮動小数点数のさまざまな精度、整数、またはBCDコードといった形式の中から1つを柔軟に選択して書き込みを行うことが可能です。
x87 FPU命令では、スタック形式で8個の汎用レジスタにアクセスできます。スタックの最上部にあるデータは常に st(0) として扱われます(図1-3の(a) ~ (d)参照)。また、st(0) からの相対オフセットで任意の汎用レジスタにアクセスすることも可能です(図1-3の(e)参照)。

x87 FPUは、以下の種類の命令をサポートしています:
- ロード命令:データを汎用レジスタスタックにプッシュします。
- ストア命令:スタック内のデータをポップし、主記憶装置に保存します。
- 演算命令:浮動小数点データの加減乗除、符号反転などを実現します。
x87 FPU命令は、以下の形式で命名されます:
f + i(省略可能) + 操作名 + p/s/l/t(省略可能)
f:命令のプレフィックス。i(省略可能):オペランドが整数であることを示します。p/s/l/t(省略可能):以下を示します:s:単精度浮動小数点数(Single Precision Floating-Point)。l:倍精度浮動小数点数(Double Precision Floating-Point)。t:拡張倍精度浮動小数点数(Double Extended-Precision Floating-Point)。p:演算後に汎用レジスタスタックからデータをポップすることを示します。
- fistpl (%rax):st(0)の拡張精度浮動小数点数を整数に変換して%raxが指すメモリに格納し、FPUスタックからデータをポップする。
- faddp %st(3), %st(0):st(3) + st(0)の結果をst(3)に格納し、st(0)をスタックからポップする。
Lab内容
- 簡易アセンブリプログラムを作成し、アセンブリを体験する。
- 提供されたアセンブリコードを用いて行列積を実装し、異なるサイズの行列に対応するようにコードを調整する。
- OSのコマンド、ファイル、および評価ツールを使用して、システム目標プロセッサのキャッシュ情報を取得する。
- perf を利用してプログラムの性能を観察する方法を学ぶ。
環境設定と事前テスト
- ツールライブラリが正しくインストールおよび設定されていることを確認する。
- アセンブリ言語の構文とコンパイルプロセスに慣れる。
実行する前に、コンピュータがインターネットに正常に接続されていることを確認してください。lab1.tar.gz をダウンロードし、ユーザーディレクトリにコピーして以下のコマンドを実行します:
tar -zxvf lab1.tar.gz
sudo apt update
sudo apt install build-essential net-tools git vim cmake gdb make gfortran libnuma-dev libtirpc-devcmake --version
gcc --version
gdb --versionsrc/lab1/print_integer.S の convert_loopに正しい終了命令を追加src/lab1/print_integer.S の print_string (48~55行目) にあるエラーを修正cd lab1
mkdir -p build && cd build
cmake -B . -S ../ && cmake --build ./ --target lab1_print_integercd dist/bins/ && ./lab1_print_integer
行列乗算のコード補完
- レジスタ間接アドレッシングとベース+インデックスアドレッシングをデモンストレーションする。
- 行列データを初期化し、アセンブリでポインタを使用する。
src/lab1/gemm_kernel.S の GEMM_INIT に適切な行列Bのアドレス保存命令を追加src/lab1/gemm_kernel.S の DO_GEMMに A[m][k] をFPUレジスタスタックにロードするロジックを追加src/lab1/gemm_kernel.S の DO_GEMMに B[k][n] をFPUレジスタスタックにロードするロジックを追加src/lab1/gemm_kernel.S の DO_GEMMに C[m][n] をFPUレジスタスタックにロードするロジックを追加mkdir -p build && cd build
cmake -B . -S ../ && cmake --build ./ --target lab1_test_gemm_kernel.unittest
./dist/bins/lab1_test_gemm_kernel.unittest --gtest_filter=gemm_kernel.test0mkdir -p build && cd build
cmake -B . -S ../ && cmake --build ./ --target lab1_gemm./dist/bins/lab1_gemm 256 256 256
CPUインフォ
未知のアーキテクチャを持つプロセッサのキャッシュ情報を取得する方法を学ぶ。
目標プロセッサのキャッシュ階層と各レベルのキャッシュサイズを取得する。
各レベルのキャッシュのセット相関数、キャッシュラインサイズを取得する。
lscpu コマンドでプロセッサモデルとキャッシュ階層情報を確認lscpu
cd /sys/devices/system/cpu/cpu0/cache
cd index0
# キャッシュラインサイズを確認
cat coherency_line_size
# セット数を確認
cat number_of_sets
# セット相関数を確認
cat ways_of_associativityPerfの使用
perf の基本的な使用方法を習得する。
perf list コマンドで対応する性能イベントを確認する。perf stat を使用して練習2の行列積プログラムのキャッシュ利用状況を確認する。
perf をインストールsudo apt install linux-tools-5.4.0-26-genericperf listlab1_gemm プログラムのキャッシュ利用状況を確認基本的な性能イベントを確認
perf stat ./dist/bins/lab1_gemm 256 256 256
# 指定した性能イベント (-e) を確認
perf stat -e L1-dcache-loads,L1-dcache-load-misses,dTLB-loads,dTLB-load-misses ./lab1_gemm 256 256 256次の実験の予習
以下を読み、高性能な行列積計算カーネルを設計する基本原則を理解し:
- Anatomy of High-Performance Matrix Multiplication
- Analytical modeling is enough for high-performance BLIS
Lab2 キャッシュ、ループ、およびブロッキングを使用して行列乗算を最適化
Lab目的
- コンピュータのキャッシュの仕組みを理解し、この仕組みを活用して行列積計算を最適化する方法を習得する。
- キャッシュを効果的に利用して行列積計算のデータアクセス経路を最適化し、命令レベルでの最適化手順を学び実践する。
- プログラムの性能ボトルネックを分析し、命令レベルでの最適化手法を理解する。
Lab前の準備
- 以下の文を読んで、高性能な行列積計算カーネルを設計する基本原則を理解してください:
- 《Anatomy of High-Performance Matrix Multiplication》
- 《Analytical modeling is enough for high-performance BLIS》
Lab原理
プリフェッチ命令 prefetch
x86-64命令セットアーキテクチャは、SSE(Streaming SIMD Extension)拡張命令を含みます。このSSE拡張命令はSIMD方式でデータの並列処理を実現し、CPUのデータ処理効率を向上させます。
プリフェッチ命令は、データをキャッシュに事前に読み込むために使用され、主な命令は以下の通りです:
| 命令名 | 機能 |
|---|---|
prefetcht0 | データをすべてのキャッシュ層(L1、L2、L3)にプリフェッチする |
prefetcht1 | データをL1キャッシュを除くすべてのキャッシュ層にプリフェッチする |
prefetcht2 | データをL1、L2キャッシュを除くすべてのキャッシュ層にプリフェッチする |
prefetchnta | 既存のキャッシュデータに影響を与えず、特定のキャッシュ層にプリフェッチする |
使用例:
prefetch<t0/t1/t2/nta> (<byte_addr>)byte_addrはバイトアドレスを表します。- プリフェッチ命令は非ブロッキングであり、プリフェッチ操作が完了するのを待たずに後続の命令を実行できます。
分割行列積とキャッシュ最適化
現在、主流の線形代数ライブラリでは、多くの場合、図2-1に示されるGotoアルゴリズムやその派生アルゴリズムを使用して行列積を計算しています。Gotoアルゴリズムの核心は、分割行列積アルゴリズムの計算手順に従って、計算に必要なデータブロックを異なるキャッシュに配置することで、データのアクセス時間を分割計算内に隠蔽することにあります。
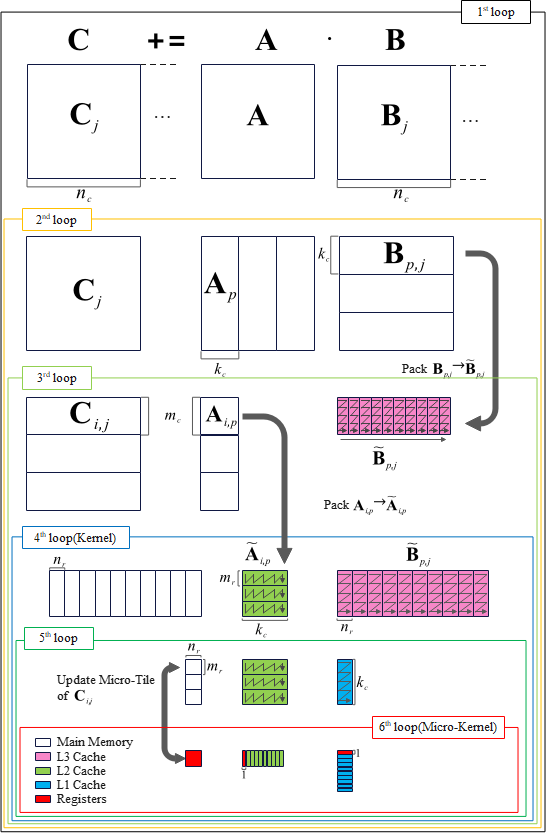
Gotoアルゴリズムの特徴:
- 図2-1に示されるように、六重ループ構造を持ちます。
- 第4層から第6層までのループは一般に「Kernel(カーネル)」と呼ばれ、計算効率を確保するため、通常は手書きのアセンブリで実装されます。
- 第6層ループの
mr、nr- これらはプロセッサコアの使用可能なレジスタ数と密接に関連しています。
- 一般に、ほとんどのデータレジスタは行列 C の分割(
mr × nrのサイズ)に割り当てられます。これにより、計算に必要な行列 A のデータを L2キャッシュ から行単位でロードし、行列 B のデータを L1Dキャッシュ からロードするための十分な時間を確保します。
- 第5層ループの
kc- ここでは、
kc × nrのサイズの行列 B のデータが L1Dキャッシュ の大部分を占めるように設定されます。 - 残りのキャッシュ容量は、行列 C と行列 A に割り当てられます。このようにすると、行列 B のデータは繰り返し利用され、L1Dキャッシュ に留まります。
- ただし、
kcが小さすぎる場合、第2層ループで行列 C の部分和の累積回数が増えます。行列 C がメモリに格納されているため、過剰な累積は計算速度を大幅に低下させます。
- ここでは、
- 第3層ループの
mcmc × kcのサイズの行列 A のデータが L2キャッシュ の大部分を占めるように設定されます。- 計算中、このデータは L2キャッシュ からレジスタへ直接流れ込みます。
- 第1層ループの
nc- 第3層ループで行列 B のデータが L3キャッシュ の大部分を占めるように選択されます。
分割とPackingについて
- 行列の分割後、分割要素のアクセスが不連続になる問題が生じる可能性があります。そのため、通常は第3層ループと第4層ループでデータをPackingして、Kernelによるアクセスの連続性と空間局所性を確保します。
- Packing はコストを伴うため、常に有益というわけではありません。柔軟なPacking戦略が、行列積計算の性能向上に寄与します。
- 主流プロセッサでは、計算ユニットとメモリアクセスユニットが独立して動作します。これにより、計算中に次回必要なデータを適切な位置に事前に準備することで、データ読み込み時間を大幅に削減し、高い計算性能を得ることができます。
- ただし、データの事前準備によってwayの競合や深刻なキャッシュエビクション(追い出し)が発生しないように注意が必要です。
高性能行列積計算の設計と最適化方法を体系的に理解するには、以下の資料を参照してください:
- Anatomy of High-Performance Matrix Multiplication
- Theory and Practice of Classical Matrix-Matrix Multiplication for Hierarchical Memory Architectures
- Analytical modeling is enough for high-performance BLIS
Lab内容
- 性能分析ツールを使用して性能ボトルネックを分析する。
- データプリフェッチ機構を利用して行列積の性能を最適化する。
- ループ展開とブロッキングを活用して計算性能を向上させる。
Perfで行列乗算パフォーマンスのボトルネックを特定
perfを使用してサンプルプログラムのキャッシュヒット率を分析する。
実行する前に、コンピュータがインターネットに正常に接続されていることを確認してください。lab2.tar.gz をダウンロードし、ユーザーディレクトリにコピーして以下のコマンドを実行します:
tar -zxvf lab2.tar.gz
mkdir -p build && cd build cmake -B . -S ../ && cmake --build ./ --target lab2_gemm_baseline
perf を使用して性能を分析:perf stat -e l2_rqsts.code_rd_hit,l1d.replacement,L1-dcache-loads,L1-dcache-load-misses ./dist/bins/lab2_gemm_baseline 256 1024 256
Prefetchを利用して行列乗算の性能を最適化する
プロセッサメーカーが提供する開発マニュアルを参照し、適切な命令を選択する方法を学ぶ(10.4.6節のデータプリフェッチ関連内容)。
命令ストリーム内でデータプリフェッチ命令の適切な配置を選定する方法を学ぶ。
- lmbench3を使用して各レベルのキャッシュのアクセスレイテンシを取得する。
- アクセスレイテンシ情報を基に、プリフェッチ命令の適切な位置を選定する。
lmbench3を使用してキャッシュのアクセス遅延を測定注意:平均値を取得するため、複数回の実行が必要です。1回の実行には約7時間かかるため、再試行回数を合理的に調整してください。
cd tools && tar xf lmbench.tgz && cd lmbench
make results設定パラメータの選択例:
- MULTIPLE COPIES [default 1]: Enterキーを押す。
- Job placement selection: 4。
- MB [default 10956]: Enterキーを押す。
- SUBSET (ALL|HARWARE|OS|DEVELOPMENT) [default all]:
HARWAREを入力。 - FASTMEM [default no]: Enterキーを押す。
- SLOWFS [default no]:
yesを入力。 - DISKS [default none]: Enterキーを押す。
- REMOTE [default none]: Enterキーを押す。
- Processor mhz [default 2688 MHz, 0.3720 nanosec clock]: Enterキーを押す。
- FSDIR [default /var/tmp]: Enterキーを押す。
- Status output file [default /dev/tty]:
/tmp/lmbench.testを入力。 - Mail results [default yes]:
noを入力。
toolsディレクトリ内のファイルがmake resultsコマンドの出力です。
実行が失敗した場合の対処手順:
LMBENCH3は新しいシステムとの互換性に問題がある可能性があるため、もし以上の選択を特定後、プログラムが異常ダウン発生。以下を実行して続行します。cp -a results ./bin/ make rerun- 実行終了を待つ。
- 結果を保存し再実行:
mv results results.bakcp -a ./bin/results ./ - レイテンシ情報を確認:
cd results && make LIST=$(../scripts/os)/*
src/lab2/gemm_kernel.Sプリフェッチ命令を追加して最適化gemm_kernel_baseline.S内のDO_GEMMコードをgemm_kernel_opt_prefetch.Sに置き換え、その上でプリフェッチ最適化コードを追加してください。
以下を実行します:
mkdir -p build && cd build
cmake -B . -S ../ && cmake --build ./ --target lab2_gemm_kernel_opt_prefetch.unittest
cd dist/bins && ./lab2_gemm_kernel_opt_prefetch.unittestmkdir -p build && cd build
cmake -B . -S ../ && cmake --build ./ --target lab2_gemm_opt_prefetch
cd dist/bins && ./lab2_gemm_opt_prefetch 1024 128 4結果を用いて、このプリフェッチ最適化の効果を評価して。その原因を説明しなさい。
ループとブロッキングを利用して行列乗算性能を向上させる
この部分は、お好きなように選んで、実装してください。
アルゴリズムの最適化を通じてキャッシュヒット率を向上させる方法を学ぶ。
キャッシュサイズに基づき行列積のブロックサイズを調整して性能を向上させる方法を学ぶ。
- プリフェッチのコードを修正し、適切なループ順序とブロックサイズを設計して、行列積の性能をさらに向上させます。
- 本練習は任意選択です。具体的な実装内容や加速効果に基づき加点評価されます。
src/lab2/gemm_kernel_opt_loop.S内のDO_GEMMプロセスの行列計算ロジックを完成させます。
以下のコマンドをプロジェクトのルートディレクトリで実行します:
mkdir -p build && cd build
cmake -B . -S ../ && cmake --build ./ --target lab2_gemm_kernel_opt_loop.unittest
./dist/bins/lab2_gemm_kernel_opt_loop.unittest以下のコマンドを実行します:
mkdir -p build && cd build
cmake -B . -S ../ && cmake --build ./ --target lab2_gemm_opt_loop
./dist/bins/lab2_gemm_opt_loop 4 32768 4- 最適化後のアルゴリズムと基準アルゴリズム(Baseline)を比較し、性能を測定します(テストケースは最適化の内容に応じて選択してください)。
- 性能結果に基づき、最適化手法の効果範囲を分析します。
次の実験の予習
以下の資料を読み、高性能行列積計算カーネルの設計原則とIntelプロセッサの特性を理解してください:
- LIBXSMM: Accelerating Small Matrix Multiplications by Runtime Code Generation
- Intel® 64 and IA-32 Architectures Software Developer’s Manual(Volume 1 & 2, Chapter 5: FPU, Chapter 14: AVX instructions)
Lab3 命令レベルの並列性、ベクトル命令、および並列処理を使用して行列乗算を最適化
Lab目的
- コンピュータシステムにおける命令レベル並列性(Instruction Level Parallelism, ILP)を理解する。
- ループ展開、ベクトル命令、多スレッド技術を活用し、現代プロセッサの多様な特性を総合的に利用してプログラム性能を最適化する方法を学ぶ。
- 命令レベル並列性、ベクトル命令、多スレッド技術を活用してプロセッサの並列性能をさらに引き出す手法を習得する。
Lab前の準備
- 以下の文を読んで、高性能な行列積計算カーネルを設計する基本原則を理解してください:
- LIBXSMM: Accelerating Small Matrix Multiplications by Runtime Code Generation
- Intel® 64 and IA-32 Architectures Software Developer’s Manual(Volume 1 & 2, Chapter 5: FPU, Chapter 14: AVX instructions)
Lab原理
データ並列処理
ベクトル命令が高速化を実現する原理は、主にSIMD(Single Instruction Multiple Data)技術に基づいています。SIMDは、1つのCPU命令で複数のデータに対して同時に操作を行うことを可能にし、大量のデータを処理する際の効率を飛躍的に向上させます。
ベクトル命令が高速化を可能にする主な原理
- 複数のデータ要素を並列処理
ベクトル命令は、プロセッサが複数のデータ要素を同時に操作できるようにします。これらのデータ要素は通常、1つのベクトルレジスタに格納されます。例えば、1つのベクトル加算命令では、2つのベクトルレジスタ内の対応する要素を同時に加算し、結果を別のベクトルレジスタに格納できます。これにより、1つの命令で複数のスカラ操作が実行され、データ処理速度が大幅に向上します。 - 効率的なメモリアクセス
ベクトル命令は通常、連続するメモリデータを効率的に処理できるように設計されています。メモリ内のデータが連続して配置されている場合、ベクトルロードおよびストア命令を使うことで、一度に複数の連続データを読み書きできます。これによりメモリアクセス回数が削減され、帯域幅の利用効率が向上します。 - 最適化されたデータパス
現代のプロセッサには、ベクトル計算専用に設計されたデータパスが組み込まれています。これらのデータパスは通常、高いスループットを持ち、ベクトル加算や乗算などの操作に特化した最適化が施されています。その結果、従来のスカラ演算よりも高速に実行できます。 - 分岐予測ミスの軽減
非ベクトルコードを実行する場合、分岐予測ミスが発生するとパイプラインが停止し、性能が低下します。一方で、ベクトル命令は通常、単純な算術論理操作に関与するため、複雑な条件判断を伴わず、分岐予測ミスによる性能低下が少なくなります。 - 命令レベル並列性(ILP)の向上
ベクトル命令は、1クロックサイクル内により多くの操作を実行することで、プロセッサの命令レベル並列性を向上させます。これにより、同時により多くの計算タスクを処理でき、全体的な性能が向上します。
SIMD命令のサポート
現代のプロセッサはほとんどがSIMD命令をサポートしています。例えば、IntelのSSEやAVX、ARMのNEONやSVEなどです。プロセッサがSIMD命令をどのようにサポートしているかについての詳細は、プロセッサメーカーが提供するユーザーマニュアルを参照してください。
データ並列処理を活用した高速化の一般的な方法には以下があります:
- ループ展開
- ベクトル命令の利用
- 共有メモリベースの並列プログラミングを実現するOpenMPライブラリの利用
1. ループ展開
パイプラインCPUの性能を最大限に引き出すには、パイプラインの停止を可能な限り減らし、フル稼働させる必要があります。そのため、命令間の並列性を十分に活用し、依存性のない命令シーケンスを見つけてパイプラインで重ねて実行する必要があります。
ループ展開(Loop Unrolling)は、ループ本体のコードを複数回コピーして順番に配置し、ループ終了条件を調整する手法です。これにより、ループの異なる反復間で存在する並列性を引き出せます。ループ展開後、ループ体のコードは結合され、コンパイラやプロセッサにより多くのスケジューリングおよび最適化の余地を提供します。また、ループ回数が大幅に減少するため、分岐命令やループ制御に伴うオーバーヘッドも削減されます。
2. AVX命令
MMX(MultiMedia eXtension)、SSE(Streaming SIMD Extension)、およびAVX(Advanced Vector Extensions)は、Intelプロセッサで使用されるSIMD命令セットです。特にAVXは、MMXやSSE命令セットを基に、128ビットのSIMDレジスタを256ビット以上に拡張し、非構造化操作や3オペランド(場合によっては4オペランド)のサポートを追加することで、命令の柔軟性と機能性を向上させています。
また、AVX命令セットは、乗加融合命令(Fused Multiply-Add, FMA)をサポートしており、1つの命令で
$$C += A \times B$$
のような乗加演算を実現できます。
AVXの環境
- 16個の256ビットベクトルレジスタ(YMM0〜YMM15)を持つ。
- 1つのAVXレジスタに、8個の32ビット単精度浮動小数点数、または4個の64ビット倍精度浮動小数点数を格納可能。
- ベクトルレジスタ内の各データフィールドは「要素(Element)」と呼ばれます(図3-1参照)。
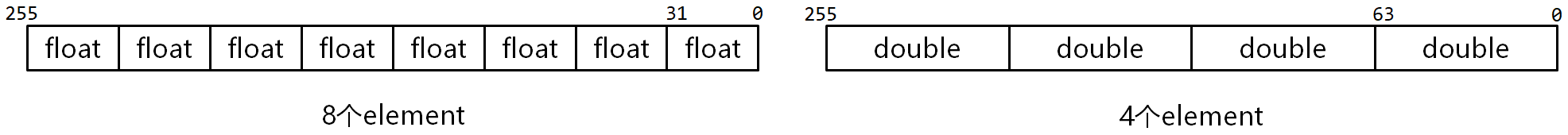
AVX命令の使用
AVX命令を使用して計算を行う際、まずデータをメモリからAVXレジスタにロードし、計算後に結果を再びメモリに保存します。
AVXの代表的な命令
| 命令 | 説明 | 使用例 |
|---|---|---|
vbroadcastssvbroadcastsdvbroadcastf128 | メモリから32/64/128ビットのオペランドを読み込み、ベクトルレジスタ内のすべての要素にブロードキャストする | vbroadcastss (%rax), %ymm0raxのアドレスでの数値をymm0で8つ同じ単精度浮動小数としてコーピ |
vmovupsvmovdquvmovapd | メモリとAVXレジスタ間で単精度浮動小数を非アライン/倍精度浮動小数を非アライン/倍精度浮動小数をアラインで移動する | vmovups %ymm0, (%rax)ymm0の8つ単精度浮動小数をraxのアドレスへ移動 |
vfmadd231psvaddpsvsubpsvmulpsvdivpsvsqrtps | 単精度浮動小数(s)で256ビットの乗加演算/加/減/乗/除/ルートを行う | vfmadd231ps %ymm0, %ymm1, %ymm2ymm2 += ymm0 * ymm1 |
OpenMP
OpenMP(Open specifications for Multi Processing)は、共有メモリ方式で多スレッド並列処理を実現するプログラミングライブラリです。OpenMPは高級言語に埋め込むことができるコンパイル指示やプリミティブを提供し、シリアルコードを並列化します。OpenMPは粗粒度から細粒度まで異なる並列化をサポートします。また、OpenMPはスレッドの使用を簡素化し、開発者がスレッドの作成、同期、負荷分散などを意識する必要がありません。
OpenMPを使った並列化の基本手順
- 計算タスクの分割
- データ転送
- サブタスク結果の統合
- サブタスク計算ロジックの実装
- スレッドの作成
詳細はOpenMP公式ドキュメントをご参照ください。
Lab内容
- プロセッサのFPUを利用し、ループ展開を組み合わせて行列積の性能を向上させる。
- AVX命令を基に、高性能な行列積計算カーネルを設計・実装する。
- OpenMPライブラリを活用し、任意の形状の行列積計算を実現する。
x87 FPUを基に行列乗算の性能を最適化する
演算ユニットの特性を活用したループ展開手法を習得します。
- データの読み取り・保存:
FLD、FSTPなどの命令を使用。 - 計算:
FMUL、FADDPなどのx87 FPUが提供する命令を使用。 - ループ展開:次元
Nのループをステップサイズ2で展開します。
実行する前に、コンピュータがインターネットに正常に接続されていることを確認してください。lab3.tar.gz をダウンロードし、ユーザーディレクトリにコピーして以下のコマンドを実行します:
tar -zxvf lab3.tar.gz
src/lab3/gemm_kernel_opt_loop_unrolling.Sで計算ロジックを実装- A[m][k] × B[k][n+1] -> st(0) の計算ロジックを追加
- C[m][n] と C[m][n+1] の読み込みロジックを追加
- C[m][n+1] + A[m][k] × B[k][n+1]の計算ロジックを追加
- C[m][n] + A[m][k] × B[k][n]の計算ロジックを追加
- C[m][n] の保存ロジックを追加
- N次元ループの更新ロジックを追加
mkdir -p build && cd build
cmake -B . -S ../ && cmake --build ./ --target lab3_gemm_opt_loop_unrolling.unittest
./dist/bins/lab3_gemm_opt_loop_unrolling.unittestmkdir -p build && cd build
cmake -B . -S ../ && cmake --build ./ --target lab3_gemm_opt_loop_unrolling
./dist/bins/lab3_gemm_opt_loop_unrolling 256 256 256- 最適化後のアルゴリズムと基準アルゴリズム(Baseline)を比較し、性能を測定します(テストケースは最適化の内容に応じて選択してください)。
- 性能結果に基づき、最適化手法の効果範囲を分析します。
AVX命令の(2m,32n,32k)高性能行列乗算計算カーネル
行列 $C$の部分行列 $C_{r}$の要素数が64以上必要(つまり$m_{r} \cdot n_{r} \geq 64$)。各次元の要件:
- $m_{r} \mod 2 = 0$
- $k_{r} \mod 8 = 0$
- $n_{r} \mod 8 = 0$
カーネルは、パイプライン設計を採用し、データの読み取り、計算、書き戻しのプロセスを実行する。
src/lab3/gemm_kernel_opt_avx.Sの概要src/lab3/gemm_kernel_opt_avx.Sは、以下の図に示すような行列ブロッキングアルゴリズムを使用します:
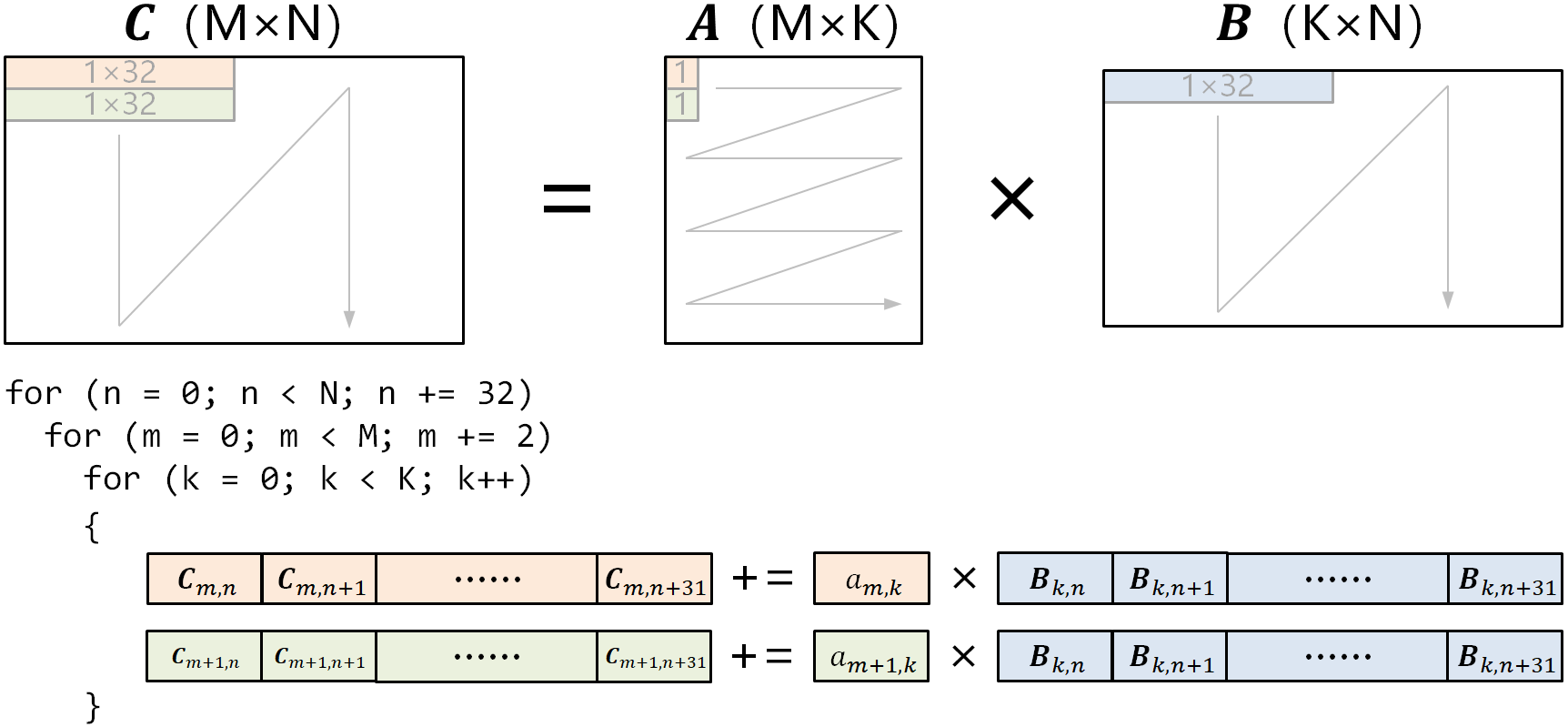
最内層ループでは、以下を計算します:
- $2 \times 1$ のブロック $A[m:m+2][k]$
- $1 \times 32$ のブロック $B[k][n:n+32]$
- 結果として $2 \times 32$ のブロック $C[m:m+2][n:n+32]$
最内層のブロック行列積は、AVXベクトル命令を用いて並列計算されます。
src/lab3/gemm_kernel_opt_avx.SでAVX命令を追加して最適化- LOAD_MAT_Cロジックを追加: 行列 $C[m:m+2][n:n+32]$ をAVXレジスタにロードします。
- LOAD_MAT_Aロジックを追加: 行列 $A[m+1][k]$ をAVXレジスタにロードします。
- LOAD_MAT_Bロジックを追加: 行列 $B[k][n:n+32]$ をAVXレジスタにロードします。
- DO_COMPUTEロジックを追加: $C[m:m+2][n:n+32]+=A[m:m+2][k]×B[k:k+8][n:n+32]$ を計算。
- STORE_MAT_Cロジックを追加: 行列 $C[m][n:n+32]$ と $C[m+1][n:n+32]$ を保存します。
以下を実行します:
mkdir -p build && cd build
cmake -B . -S ../ && cmake --build ./ --target lab3_gemm_opt_avx.unittest
./dist/bins/lab3_gemm_opt_avx.unittestmkdir -p build && cd build
cmake -B . -S ../ && cmake --build ./ --target lab3_gemm_opt_avx
./dist/bins/lab3_gemm_opt_avx 256 256 256最適化後のアルゴリズムと基準アルゴリズム(Baseline)を比較し、性能を測定します(テストケースは最適化の内容に応じて選択してください)。
性能結果に基づき、最適化手法の効果範囲を分析します。
OpenMPとAVX命令で任意形状の行列乗算を実現する
この部分は、お好きなように選んで、実装してください。
行列積がマルチスレッドで以下の形状に対応する必要があります:
- $M \geq 2$, $K \geq 8$, $N \geq 8$
分割後に練習2カーネルの要件を満たさないデータブロックに対しては、Paddingまたは別途設計したカーネルで計算を実施することが可能です。
各次元の並列化戦略を独自に設計します。ただし、使用するスレッド数は関数のパラメータで指定された最大スレッド数を超えてはいけません。
計算性能はベースラインを上回る必要があります。
- 異なるレベルの並列化戦略を活用し、プログラムの性能を向上させる手法を学びます。
- 本練習は任意選択です。具体的な実装内容や加速効果に基づき加点評価されます。
src/lab3/openmp_gemm_baseline.cppの概要src/lab3/openmp_gemm_baseline.cppは、以下に示すようなマルチスレッド行列ブロッキングアルゴリズムを使用します:

- 6行目~13行目:
get_parallel_thread_num関数は、最大スレッド数max_threadsを使用して、行列Aの行ブロック数m_threadおよび行列Bの列ブロック数n_threadを計算します。行列Aは最大2つのブロックに分割されます。 - 15行目:
openmp_gemm_baseline関数のthread_numパラメータは、計算に使用する最大スレッド数を表します(コマンドライン引数で指定可能)。 - 22行目~26行目: OpenMPのディレクティブを使用して、スレッド数、共有変数(行列C)、プライベート変数などの情報を設定します。
- 27行目~100行目: 各スレッドが実行するコードです。
- 29行目: スレッドIDを取得します(最初のスレッドIDは0、次は1と順に割り振られます)。
- 31行目~32行目: スレッドIDを、行列Aの行ブロック番号
thread_id_mと行列Bの列ブロック番号thread_id_nにマッピングします。- 例えば、IDが6のスレッドが行ブロック番号1と列ブロック番号2に対応する場合、スレッド6は行列Aの1番目の行ブロックと行列Bの2番目の列ブロックの行列積を計算します。
- 36行目~41行目: 行列Aの各行ブロックの行数
dim_m_per_thread、行列Bの各列ブロックの列数dim_n_per_threadを計算します。 - 48行目~52行目: 行列Aの
thread_id_m番目の行ブロックの開始行番号thread_m_startと終了行番号thread_m_endを計算します。 - 55行目~59行目: 行列Bの
thread_id_n番目の列ブロックの開始列番号thread_n_startと終了列番号thread_n_endを計算します。 - 62行目~67行目: ブロックサイズに応じたメモリを割り当てます。
- 70行目~84行目: スレッドIDに対応する行ブロック番号
thread_id_mと列ブロック番号thread_id_nを基に、対応するブロックデータを元の行列A、B、Cから一時行列A_padding、B_padding、C_paddingにコピーします。 - 87行目~95行目: 練習2で実装した
gemm_kernel_opt_avxカーネルを呼び出し、ブロック行列積を計算し、計算結果を元の行列Cに保存します。
src/lab3/openmp_gemm_opt.cppでロジックを実装OpenMPライブラリを利用して、マルチコアに対応し、より大規模な行列積計算をサポートするアルゴリズムを設計します。
以下のコマンドをプロジェクトのルートディレクトリで実行します:
mkdir -p build && cd build
cmake -B . -S ../ && cmake --build ./ --target lab3_gemm_opt_openmp.unittest
./dist/bins/lab3_gemm_opt_openmp.unittest以下のコマンドを実行します:
mkdir -p build && cd build
cmake -B . -S ../ && cmake --build ./ --target lab3_gemm_opt_openmp
./dist/bins/lab3_gemm_opt_openmp 8 512 512 512- 最適化後のアルゴリズムと基準アルゴリズム(Baseline)を比較し、性能を測定します(テストケースは最適化の内容に応じて選択してください)。
- 性能結果に基づき、最適化手法の効果範囲を分析します。
レポートの要件
Lab1~Lab3を完了し、以下の要件に従ってレポートを作成してください。
レポートの形式にはテンプレートはありませんが、次の内容を含めるようにしてください。
Labsのプロセス
図表を組み合わせ、文章形式で表現してください。
テスト結果と原理の分析
図表、文章、ソースコードを用いて以下を比較分析してください:
- キャッシュ最適化とデータ並列化最適化の効果を比較する
- その原理を説明する
レポートをPDF形式で、宿題システムにアップロードしてください。
以下のソースファイル(3つから5つ)を.zip形式に圧縮し、宿題システムにアップロードしてください。
- Lab2:
- 練習2:
gemm_kernel_opt_prefetch.S - 練習3(あるなら):
gemm_kernel_opt_loop.S
- 練習2:
- Lab3:
- 練習1:
gemm_kernel_opt_loop_unrolling.S - 練習2:
gemm_kernel_opt_avx.S - 練習3(あるなら):
openmp_gemm_opt.cpp
- 練習1:
次の実験の予習
以下の資料を読み、CUDAプログラミングやGPUの特性を理解してください:
Lab4 CUDA:GPUの行列乗算
Lab目的
- C/CUDAプログラミングを使用して行列積を実装する方法を習得する。
- GPUのマルチスレッド並列計算能力を活用し、プログラムの性能を向上させる方法を学ぶ。
- CUDAの基本的なプログラミングモデルとスレッドスケジューリング手法を習得し、GPU上で効率的な行列演算を実現することで、計算デバイスの並列処理能力をさらに引き出す方法を理解する。
Lab前の準備
- 以下の資料を読み、CUDAプログラミングの基本原理とGPUアーキテクチャの特性を理解して、高効率な行列積計算を実現してください。
Lab原理
このLabでは、CUDA(Compute Unified Device Architecture)を使用した並列プログラミングを学び、行列積計算を高速化します。CUDAはNVIDIAが提供する並列計算プラットフォームおよびプログラミングモデルであり、NVIDIA GPUの計算能力を活用して大規模な並列計算タスクを処理できます。CUDAを使用することで、行列積の計算性能を大幅に向上させ、大規模な行列を効率的に処理することが可能になります。
行列積の概要
2つの行列 $A$ と $B$ の積行列 $C$ の各要素は、以下の式で計算されます。$$C_{ij} = \sum_{k=1}^n A_{ik} \cdot B_{kj}$$
ここで、$C_{ij}$ は行列 $C$ の $i$ 行 $j$ 列の要素を表します。行列 $C$ の各要素を計算するためには、行列 $A$ の行と行列 $B$ の列を順に走査する必要があり、その計算量の時間計算量は $O(m \times n \times p)$ です。大規模な行列の場合、計算量が非常に多くなります。
CUDAによる行列積計算の高速化原理
CUDAはGPUの大規模並列計算アーキテクチャに基づいており、複数のスレッドが協力して効率的にデータを処理します。以下はCUDAを使用した行列積高速化の主な原理です。
- 多スレッドによる並列計算
CUDAはGPU上の数千から数万の並列スレッドを使用して計算を高速化します。行列積では各要素の計算が相互に独立しているため、CUDAは各計算タスクを1つのスレッドに割り当て、同時に複数のスレッドが計算を実行することで、計算効率を大幅に向上させます。 - ブロックとグリッド構造
CUDAでは、スレッドは「スレッドブロック」と「グリッド」によって編成されます。各スレッドブロックは行列の一部を担当し、中間計算結果を共有メモリに保存します。この階層構造により、メモリ管理と並列処理が効率化されます。たとえば、スレッドブロック内の各スレッドは結果行列の1つの要素計算を担当します。 - メモリ遅延の隠蔽
GPUは非常に多くのスレッドを持ち、それらが切り替わることでメモリ遅延を隠蔽します。一部のスレッドがメモリ読み取りでブロックされている間、他のスレッドが計算を続行するため、計算ユニットの利用率を高めることができます。 - 命令レベル並列性(ILP)
CUDAアーキテクチャは、各クロックサイクルで複数の命令を実行できます。命令パイプラインを並列実行経路に最適化することで、行列積などの計算タスクを加速し、同時により多くの操作を実行して全体的な計算効率を向上させます。 - 計算集約型とメモリ集約型のバランス
CUDAはスレッド数、ブロックサイズ、メモリ割り当て戦略を調整することで、計算とメモリアクセスのバランスを最適化し、GPUリソースを効率的に活用します。
図4-1に示すように、各スレッドが結果行列 $P$ の1つの要素を計算します。行列 $M$ と行列 $N$ はそれぞれグローバルメモリに格納されます。各スレッドは、グローバルメモリから $M$ の1行と $N$ の1列を読み取り、内積計算を実行して $P$ の1つの要素を求めます。
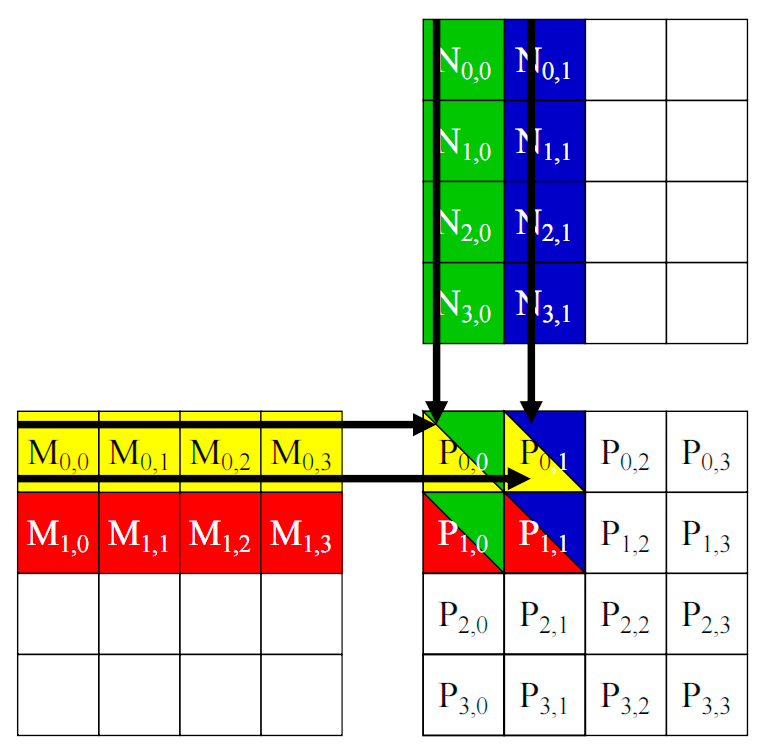
CUDAの並列処理技術を利用することで、行列積のような計算集約型タスクを大幅に高速化でき、科学計算や画像処理などの分野で広く利用されています。
GPUアーキテクチャの概要
GPUは主にストリームプロセッサアレイとメモリシステムで構成されています。その構造は図4-2に示されています。
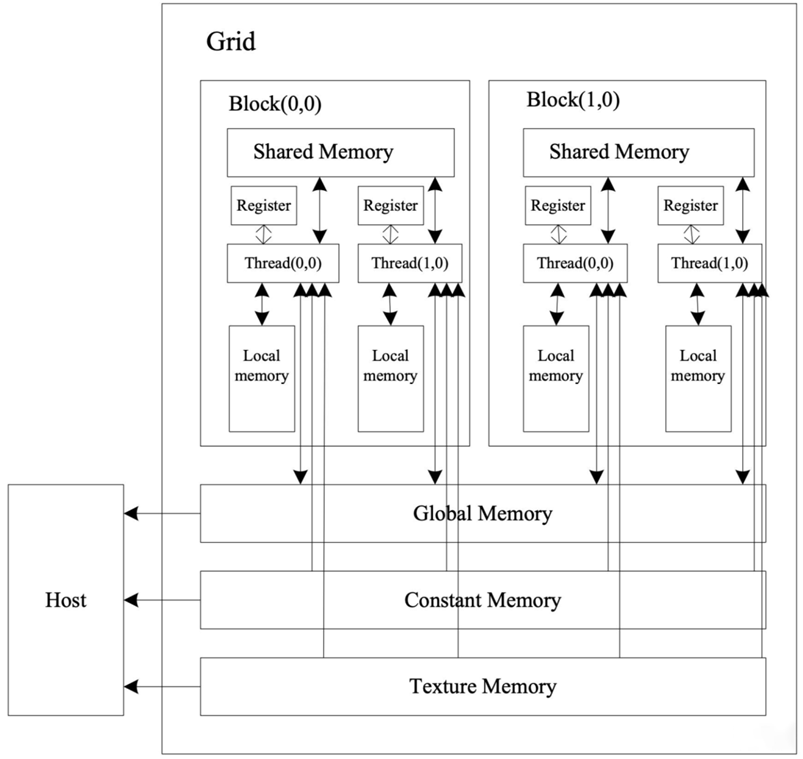
- 各ストリームプロセッサは、GPUのスレッド(Thread)と呼ばれます。
- すべてのスレッドは「グリッド(Grid) – スレッドブロック(Block) – スレッド(Thread)」の階層構造で編成されています。
- GPU内には複数のグリッドが含まれ、各グリッドは複数のブロックで構成され、各ブロックは複数のスレッドを持ちます。この構造は、アプリケーションの要件に応じて、2次元、3次元、さらにはそれ以上の次元で編成できます。
各スレッドにはプライベートなレジスタとローカルメモリ(Local Memory)があり、同じブロック内のすべてのスレッドはスレッドブロック内の共有メモリ(Shared Memory)を共有します。すべてのブロックは、グローバルメモリ(Global Memory)、定数メモリ(Constant Memory)、およびテクスチャメモリ(Texture Memory)を共有し、これらのメモリはデータ局所性を考慮して最適化されています。計算中、ホスト(Host)は、まず処理対象のデータをこれらのメモリにバッチ転送し、計算終了後に結果をメモリから読み取ります。
CUDAプログラムの基本構成
CUDAプログラムは主にホストコード(Host Code)とカーネル関数で構成されます。
- ホストコードは、CPU(Host)上で実行されるC/C++プログラムで、メモリの確保、データの前処理、データ転送、CUDAスレッド数の割り当て、カーネル関数の呼び出しなどを行います。
- カーネル関数は、GPU(Device)のハードウェアスレッド(コア)上で実行されるコードであり、そのためカーネル関数と呼ばれます。
以下に、行列加算のCUDAサンプルプログラムを示します。
// Deviceカーネル関数(GPUのハードウェアスレッド上で実行)
__global__ void matrixAdd(float A[Ny][Nx], float B[Ny][Nx], float C[Ny][Nx])
{
// 行列要素の行番号と列番号を取得
int row = blockIdx.y * blockDim.y + threadIdx.y;
int col = blockIdx.x * blockDim.x + threadIdx.x;
C[row][col] = A[row][col] + B[row][col];
}
// Hostコード(CPU上で実行)
int main()
{
......
const int Nx = 12;
const int Ny = 6;
// 1つのBlockに4×3のThreadを定義
dim3 threadsPerBlock(4, 3);
// 1つのGridに3×2のBlockを定義
dim3 numBlocks(Nx/threadsPerBlock.x, Ny/threadsPerBlock.y);
// カーネル関数を呼び出し(6ブロック×12スレッド=72スレッド並列実行)
matrixAdd<<<numBlocks, threadsPerBlock>>>(A, B, C);
......
}コードの説明
- 2行目:
__global__キーワードを使用してカーネル関数を宣言します。 - 5~6行目:BlockとThreadのサイズ属性を使用して行列要素の行番号と列番号を計算します。
blockIdxは現在のカーネル関数が実行されるスレッドが属するBlockのインデックスを表します。blockIdx.xとblockIdx.yは、それぞれBlockのx軸方向とy軸方向の座標を示します。blockDimは現在のBlockのサイズを示し、blockDim.xとblockDim.yは、それぞれBlockの列数と行数を表します。threadIdxも同様です。
- 14~18行目:変数の定義、メモリの確保、データの前処理、データ転送などを行います。
- 20~22行目:GridとBlockのサイズを定義します。
- 24行目:定義したGridとBlockのパラメータを使用してカーネル関数を呼び出し、行列加算を実行します。
Lab内容
GPUの行列乗算
GPUプログラミングモデルに慣れる。
CPUによる行列積の実装の考え方を学ぶ。
CUDAファイルのコンパイルと実行プロセスを習得する。
- GPUによる行列積の結果の正確性を検証する。
- 異なるサイズの行列積をテストし、実験結果を観察する。
実行する前に、コンピュータがインターネットに正常に接続されていることを確認してください。lab4-5.tar.gz をダウンロードし、ユーザーディレクトリにコピーして以下のコマンドを実行します:
tar -zxvf lab4-5.tar.gz
lab4-5ディレクトリ内のテンプレートコードmatrix_mul.cuを開きます。MatrixMulKernel関数の下にCUDA行列積のコードを実装します。- 結果行列の位置インデックスを計算
- 各スレッドが行列 $C$ の1つの要素の値を計算します。結果行列 $C$ の各要素を計算するループを実装しなさい。
- 計算結果を対応する位置の結果行列に割り当て。
- 関数呼び出しの確認:
main関数 でMatrixMulKernel関数が呼び出されている。
bash compile.sh
./a.out 1 1000Total Errors = 0の場合、カーネルが正確。
GPUでの行列積の計算時間 と 計算結果の正確性 を確認します。
- 行列のサイズを変更してテストします。
- スレッドブロックサイズ
TILE_SIZEを変更してテストします(スレッドブロックも正方形)。 - 異なるパラメータ設定下で計算結果と性能を比較 し、最適な設定を考察します。
次の実験の予習
以下の資料を読み、CUDAにおける共有メモリを使用した行列積の最適化の基本原理を理解してください:
Lab5 CUDA:GPUの行列乗算最適化
Lab目的
- CUDAの共有メモリを利用した最適化技術を習得し、行列積の性能を向上させる方法を理解する。
- GPUプログラムの性能ボトルネックを分析する方法を習得する。
- 共有メモリを活用してデータアクセス経路を最適化する手法を学ぶ。
Lab前の準備
- 以下の資料を読み、CUDAにおける共有メモリを使用した行列積の最適化の基本原理を理解してください:
- Lab環境:CUDA Toolkit、NVIDIAドライバー、および関連開発ツール(
nvcc、cuda-gdbなど)がインストールされているコンピュータ。
Lab原理
CUDA共有メモリ最適化
共有メモリ(Shared Memory)は、CUDAアーキテクチャにおいて、各ストリーミングマルチプロセッサ(Streaming Multiprocessor, SM)内に配置された高速キャッシュであり、同じスレッドブロック内のスレッド間でデータを共有するために使用されます。共有メモリはグローバルメモリと比較してアクセス速度が非常に速いため、頻繁に同じデータにアクセスする必要がある場合に、性能を大幅に向上させることができます。共有メモリを活用して再利用するデータを事前にロードすることで、グローバルメモリへのアクセス回数を減らし、遅延を低減し、帯域幅の利用効率を向上させることができます。
共有メモリの高速化原理は、次の重要なポイントに集約されます:
1. 高速なアクセス速度
- 共有メモリはCUDAの各ストリーミングマルチプロセッサ上に配置されており、アクセス遅延が非常に低く、グローバルメモリよりも遥かに高速です。
- 頻繁にアクセスするデータを格納するのに適しており、計算処理の効率を向上させます。
2. スレッドブロック内での共有
- 共有メモリは、同じスレッドブロック内のすべてのスレッドによってアクセスおよび共有することができます。
- 複数のスレッドが協調して作業し、同じデータを繰り返し読み取る必要がなくなるため、メモリアクセスにかかる時間を削減できます。
図5-1に示すように、共有メモリは各スレッドブロック内に配置されており、同じブロック内のすべてのスレッドが高速にデータを共有できます。これにより、グローバルメモリへのアクセス回数が減少し、遅延が軽減され、メモリ帯域幅の利用効率が向上します。共有メモリは特に、複数のスレッドが頻繁に同じデータを必要とする計算処理において、非常に効果的です。
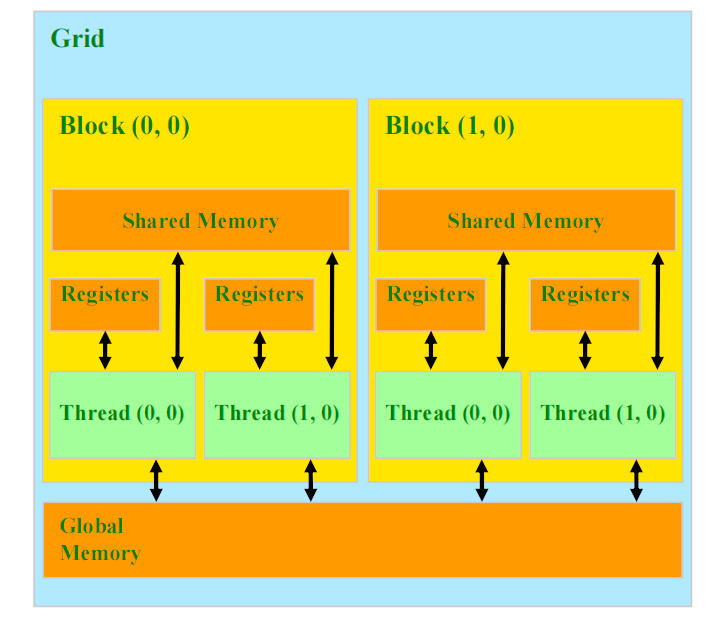
Lab内容
共有メモリでのGPU行列乗算最適化
共有メモリを使用してグローバルメモリへのアクセスを減らし、データアクセス効率を向上させる方法を学ぶ。
共有メモリサイズに基づいて行列ブロックサイズを最適化し、計算性能を向上させる方法を理解する。
- CUDAの共有メモリメカニズムを使用して行列積アルゴリズムを最適化し、最適化前後の計算時間と効率を比較する。
- BLOCKSIZEのサイズを調整し、異なるBLOCKSIZEが計算効率に与える影響を比較する。
以下のコードをLab4からのmatrix_mul.cuのMatrixMulSharedMemKernel関数に貼り付けてください。
// Block index
int bx = blockIdx.x;
int by = blockIdx.y;
// Thread index
int tx = threadIdx.x;
int ty = threadIdx.y;
// Index of the first sub-matrix of A processed by the block
int aBegin = wA * BLOCK_SIZE * by;
// Index of the last sub-matrix of A processed by the block
int aEnd = aBegin + wA - 1;
// Step size used to iterate through the sub-matrices of A
int aStep = BLOCK_SIZE;
// Index of the first sub-matrix of B processed by the block
int bBegin = BLOCK_SIZE * bx;
// Step size used to iterate through the sub-matrices of B
int bStep = BLOCK_SIZE * wB;
// Csub is used to store the element of the block sub-matrix
// that is computed by the thread
float Csub = 0;
// Loop over all the sub-matrices of A and B
// required to compute the block sub-matrix
for (int a = aBegin, b = bBegin;
a < aEnd;
a += aStep, b += bStep) {
// Declaration of the shared memory array As used to
// store the sub-matrix of A
__shared__ float As[BLOCK_SIZE][BLOCK_SIZE];
// Declaration of the shared memory array Bs used to
// store the sub-matrix of B
__shared__ float Bs[BLOCK_SIZE][BLOCK_SIZE];
// Load the matrices from device memory
// to shared memory; each **thread** loads
// one element of each matrix
// --- TO DO :Load the elements of the sub-matrix of A into As ---
// --- Load the elements of the sub-matrix of B into Bs ---
// NOTE: Ensure that the thread indices do not exceed the matrix dimensions to avoid out-of-bounds access.
// Use boundary checks to load valid elements into shared memory, and set invalid elements to 0.0f
// Synchronize to make sure the matrices are loaded
__syncthreads();
// Multiply the two matrices together;
// each thread computes one element
// of the block sub-matrix
#pragma unroll
// --- TO DO :Implement the matrix multiplication using the sub-matrices As and Bs ---
// Synchronize to make sure that the preceding
// computation is done before loading two new
// sub-matrices of A and B in the next iteration
__syncthreads();
}
// Write the block sub-matrix to device memory;
// each thread writes one element
int c = wB * BLOCK_SIZE * by + BLOCK_SIZE * bx;
// --- TO DO :Store the computed Csub result into matrix C ---
// NOTE: Ensure that the thread indices "c" do not exceed the matrix dimensions to avoid out-of-bounds access.
// Use boundary checks to write valid elements to the output matrix C.テンプレートコードの実装概要
テンプレートコードでは、以下のようにスレッドと行列要素の対応関係を定義しています:
- 各スレッドが行列 $C$ の1つの要素を計算します。
- 各スレッドブロックが行列の1つのブロックを担当し、スレッドブロック内のスレッドがブロック内の各要素を計算します。
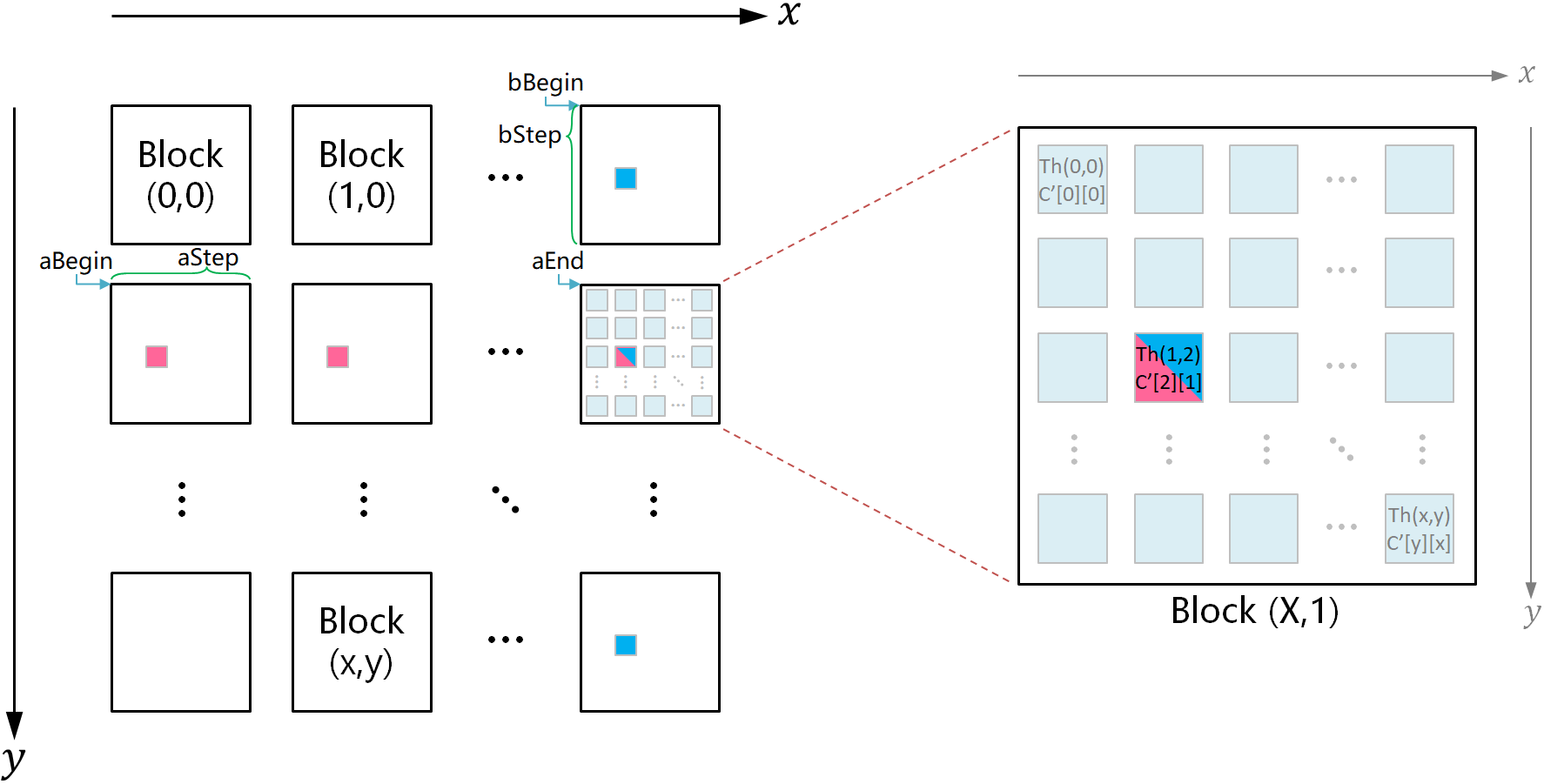
右図は、左図の第2行最後の列にあるスレッドブロックに対応する分割行列を表します。
例えば、$C'[2][1]$ はその分割行列の3行目2列目の要素を示します。他の要素も同様に対応します。
計算の際、各スレッドは行列 $A$ および $B$ からスレッドブロック内の特定位置に対応する要素を1つずつロードします。
例えば、図のスレッド Thread(1,2) は、最初のループでは図の aBegin が指し示す分割行列から $A'[2][1]$、bBegin が指し示す分割行列から $B'[2][1]$ をロードします。
2回目のループでは、aBegin + aStep が指し示す分割行列から $A'[2][1]$、bBegin + bStep が指し示す分割行列から $B'[2][1]$ をロードし、この処理を繰り返します。
スレッド Thread(i,j) は各ループで $A'[j][i]$ と $B'[j][i]$ の2つの要素をロードするだけですが、計算で必要な $A'[j][k]$ および $B'[k][i]$ のすべての要素$0 \leq k < \text{BLOCK\_SIZE}$は、スレッドブロック内の他のスレッドによって並列的に共有メモリにロードされます。このため、Thread(i,j) は正確に $C'[j][i]$ を計算することが可能です。
実装を簡略化するため、行列要素のインデックスを「スレッドブロックインデックス」と「ブロック内スレッドインデックス」の2段階に分けて考えます。
- スレッドブロックインデックス
これはスレッドブロック左上のスレッドのインデックスです。 - ブロック内スレッドインデックス
ブロック内のスレッドがスレッドブロックインデックスからどれだけずれているかを示します。
図から分かるように、$C'[2][1]$ は $(X,1)$ 番目のスレッドブロック内の $(1,2)$ 番目のスレッドによって計算されます。
行列 $C$ の列数 $N$ とスレッドブロックの辺長 $\text{BLOCK\_SIZE}$ を組み合わせることで以下が得られます:
- スレッドブロック(X,1)の2次元インデックス:\[[1\times\text{BLOCK\_SIZE}][X\times\text{BLOCK\_SIZE}]\]
- スレッドブロック(X,1)の1次元インデックス:\[(1\times N + X)\times \text{BLOCK\_SIZE}\]
また、ブロック内スレッドの座標 $(1,2)$ から以下を導き出せます:
- ブロック内スレッドの2次元インデックス:$[2][1]$
- ブロック内スレッドの1次元インデックス:$2\times N + 1$
これらを加算すると、$C'[2][1]$ が行列 $C$ に対応する全体的な2次元インデックスは:\[[1*\text{BLOCK\_SIZE} + 2][X*\text{BLOCK\_SIZE} + 1]\]
全体的な1次元インデックスは:\[(1\times N + X)\times\text{BLOCK\_SIZE} + 2\times N + 1\]
共有メモリへのデータ読み取り
- 各スレッドが行列 $A$ と $B$ の要素をそれぞれ共有メモリ
As[ty][tx]、Bs[ty][tx]にロードします。 - 境界条件を確認し、範囲外アクセスを防止するため、有効な要素のみを読み取り、無効な要素には
0.0fを設定します。
行列 $C$ の計算
forループを使用して共有メモリAsとBsを使い、対応する要素を掛け算し、累積してCsubに保存します。
計算結果の書き戻し
- ブロックインデックス
(bx, by)とスレッドインデックス(tx, ty)を使用して、行列 $C$ のグローバル位置を計算します。 - 書き戻し前にグローバルインデックスが行列 $C$ の有効範囲内であることを確認します。
main関数の変更
forループを変更し、MatrixMulSharedMemKernel関数を呼び出すようにします。
bash compile.sh
./a.out 1 1000Total Errors = 0の場合、カーネルが正確。
一部のGPUの計算精度が低いの場合、つまり数値誤差が0.5以内であれば、切上、切下のロジックを追加して補正可能です。
GPUでの行列積の計算時間 と 計算結果の正確性 を確認します。Lab4の計算性能と比較して下さい。
- 行列のサイズを変更してテストします。
- スレッドブロックサイズ
TILE_SIZEを変更してテストします(スレッドブロックも正方形)。 - 異なるパラメータ設定下で計算結果と性能を比較 し、最適な設定を考察します。
CUBLASでのGPU行列乗算最適化
cublasSgemmはCUDAのcuBLASライブラリの行列積演算関数で、以下のように行列計算を行います:\[C = \alpha \cdot A \cdot B + \beta \cdot C\]
詳細な使用方法は以下を参照してください:CUDA cuBLAS Documentation – GEMM
matrix_mul.cu先頭の#define USE_CUBLASを起用してください。
main関数の変更
forループを変更し、cublasSgemm関数を呼び出すようにします。
bash compile.sh
./a.out 0 1000- 行列のサイズを変更してテストします。
- スレッドブロックサイズ
TILE_SIZEを変更してテストします(スレッドブロックも正方形)。
レポートの要件
Lab4~Lab5を完了し、以下の要件に従ってレポートを作成してください。
レポートの形式にはテンプレートはありませんが、次の内容を含めるようにしてください。
Labsのプロセス
図表を組み合わせ、文章形式で表現してください。
テスト結果と原理の分析
図表、文章、ソースコードを用いて以下を比較分析してください:
- 入力行列のサイズおよびスレッドブロックのサイズがCUDA行列積計算結果に与える影響を分析、その原理を説明しなさい。
- 共有メモリ最適化前後の実行結果を比較し、関連する原理を詳しく説明してください。
レポートをPDF形式で、宿題システムにアップロードしてください。
以下のソースファイル(1つ、または2つ)を.zip形式に圧縮し、宿題システムにアップロードしてください。
1つのファイルに実験4と実験5のコードが含まれている場合はその1つのファイルだけを提出してください。
別々のファイルで実装されている場合は、2つのファイルを提出してでもいい。
- Lab4~5:
matrix_mul.cu
Lab6 LLaMAの最適化
Open Project
Lab目的
- 学んだ行列積最適化手法を総合的に活用し、中規模モデルの推論性能を向上させる方法を習得する。
- コンピュータアーキテクチャに関連する原理と技術が実際のアプリケーションでどのように活用されるかを理解する。
Lab内容
Llama2は、Transformerアーキテクチャに基づく軽量オープンソースの自然言語処理モデルです。推論と量子化は単一のCプログラムで実装され、豊富なコメントが含まれており、移植、展開、最適化が容易です。
この実験は自由度の高いオープン形式の内容です。これまでの実験で学んだ行列積最適化手法から自由に選択および組み合わせを行い、最適化された行列積アルゴリズムをLlama2モデルに統合することで、推論性能を向上させます。
具体的なタスクは以下の通りです:
- Llama2の推論プログラムを読み、行列積の実装方法を理解し、分析やデバッグによって行列積演算のデータ規模を把握する。
- 最適化手法を1つ選択する、または複数の最適化手法を組み合わせて、Llama2の行列積性能を向上させる。
- 異なるサイズのLlama2モデルを実行し、最適化前後の推論性能を比較し、合理的に分析する。
- 最適化後の推論速度が最適化前と比較して安定した性能向上を示した場合、追加得点が得られます(得点は最適化効果に基づいて判断)。
実行する前に、コンピュータがインターネットに正常に接続されていることを確認してください。llama2.c.tar.gz 、stories15M.bin、stories42M.bin、stories110M.binをGitHubとHuggingFace(stories15M.bin, stories42M.bin, stories110M.bin)から又はキャンパスネットからダウンロードし、ユーザーディレクトリにコピーして以下のコマンドを実行します:
tar -zxvf llama2.c.tar.gz
ダウンロードした .binを解凍後の llama2.c/ ディレクトリに配置します。mv stories15M.bin llama2.cmv stories42M.bin llama2.cmv stories110M.bin llama2.c
ターミナルを開き、llama2.c/ ディレクトリに移動します。
以下のコマンドでコードをコンパイルします:
make run以下のコマンドを実行してLlama2モデルを動作させます:
./run stories15M.bin次に、異なるサイズのモデルを実行します:
./run stories42M.bin
./run stories110M.binモデルサイズに応じた実行時間の違いを観察しなさい。
Llama2の推論処理は run.cに実装されています。
行列積関数は matmul にあり。コメントによると、matmul 関数は $d \times n$ の行列 $W$ と次元 $n$ の列ベクトル $x$ の積を計算します。また、推論処理の性能ボトルネックはこの行列積関数にあることが示されています(興味がある場合は、デバッグで確認可能です)。
お好きな方法で(コード内に printf 文を追加する、または GDB などのデバッグツールを使用して)matmul 関数の入力行列のサイズを確認しなさい。
matmul関数を最適化するこれまでの実験で実装した行列積最適化アルゴリズムを変更し、run.c 又はrun.cuに統合します。
コードを変更した後、以下のコマンドでコンパイルして実行します:
- CUDA最適化を使用する場合:
nvcc -O3 -o run run.cu -lm - cuBLASライブラリを使用する場合:
nvcc -O3 -o run run.cu -lm -L/usr/local/lib64 -lcublas - OpenMPを使用する場合:
gcc -O3 -o run run.c -lm -fopenmp - AVXなど他のCPU向けの最適化手法を使用する場合:
make run
- 各
.binファイルを使用して最適化前後のLlama2モデルをそれぞれ3~5回実行します。 - 推論速度の平均値を記録し、最適化前の結果と比較します。
- 結果を分析し、さらに改善の可能性を検討します。
以下はCUDA最適化を使用した例です:
レポートの要件
Lab6を完了し、以下の要件に従ってレポートを作成してください。
レポートの形式にはテンプレートはありませんが、次の内容を含めるようにしてください。
Labのプロセス
図表を組み合わせ、文章形式で表現してください。
テスト結果と原理の分析
図表、文章、ソースコードを用いて以下を比較分析してください。
採用した最適化手法の原理についても詳しく説明してください。
レポートをPDF形式で、宿題システムにアップロードしてください。
Lab中に変更したファイルを .zip 形式に圧縮し、宿題システムにアップロードしてください。
以上です



コメント