0. 紹介
Not now.
1. 必要な知識
1.1 概念
| Name | Explanation | Sample |
| アルファベット | 文字の非空有限集合 | $\Sigma = \{a, b, c, \cdots \}$ |
| 文字列 | あるアルファベットの有限長シーケンス | $aabcab$ |
| 文字列の長さ | 文字列の字数 | $aabcab$の長さは6 |
| $\varepsilon$ | 空文字列 | 長さ0の文字列 |
| 文字列の接続 | concatenate操作、オペレーターは$\cdot$ | $x\cdot y = xy$, $x\varepsilon=x$ |
| 文字列のベキ | 繰り返し接続 | $x^3=xxx$,$x^0=\varepsilon$, $\varepsilon^n = \varepsilon$ |
| 言語 | あるアルファベットの特定文字列集合 | $L=\{\varepsilon,aa,bb,cc,\cdots\}$ $\varnothing$,$\{\varepsilon\}$は任意アルファベットの言語 |
| 言語の接続 | concatenate操作、オペレーターは$\cdot$ | $LR=\{w=xy|x\in L\land y\in R\}$ |
| 言語のベキ | 繰り返し接続 | $L^2=\{w=xy|x\in L\land y\in L\}$ $L^0=\{\varepsilon\}$ |
| クリーネ閉包 | 全(*)閉包、反射推移閉包 | $\Sigma^*=\bigcup\limits_{i=0}^{\infty}\Sigma^i$ |
| 正規閉包 | 正閉包、推移閉包 | $\Sigma^+=\bigcup\limits_{i=1}^{\infty}\Sigma^i$ |
1.2 諸性質
$\Sigma^*=\{\varepsilon\}\cup\Sigma^+$
$\varnothing^+=\varnothing$
$\varnothing^*=\{\varepsilon\}$
$(L^+)^+=L^+$
$(L^*)^*=L^*$
$L^+ \cup R^+ \subseteq (L\cup R)^+$
$L^* \cup R^* \subseteq (L\cup R)^* = (L^*R^*)^*= (R^*L^*)^*$
1.3 小テスト
I.アルファベット $\Sigma= \{a,b\}$ とすると、クリーネ閉包$\Sigma^*$の元の長さは__
(A) 0、有限数、または無限大。
(B) 無限大のみ
(C) 無限大または有限数
(D) 有限数のみ
II.アルファベットのクリーネ閉包は無限集合でなければならない。
(A) True
(B) False
III.$\forall\Sigma(\Sigma$はアルファベット$\rightarrow \Sigma^*\neq \Sigma^+)$
(A) True
(B) False
IV.$\forall S(S$は集合$\rightarrow S^*\neq S^+)$
(A) True
(B) False
1.4 Answer
I.D
II.B
III.A
IV.B
1.5 検定問題
1.{$\varepsilon$, 0, 00}の冪集合を求め
$\{\varnothing, \{\varepsilon\}, \{0\}, \{00\}, \{\varepsilon, 0\}, \{\varepsilon, 00\}, \{0, 00\}, \{\varepsilon, 0, 00\}\}$
2.次の式の正誤を判断。
(1) False
(1) $(LR)^*=(RL)^*$
(2) $L^+=L^+L^+$
(3) $L^*=L^*L^*$
(4) $(L\cup R)^*=R^*\cup L^*$
(5) $(LR\cup L)^*L=L(RL\cup L)^*$
(6) $R(LR\cup R)^*L=LL^*R(LL^*R)^*$
(7) $(L^+)^*=(L^*)^+=L^*$
(8) $L^*L^+=L^+L^*=L^+$
(2) False
(3) True
(4) False
(5) True
(6) False
(7) True
(8) True
2. 有限オートマトン
2.1 決定的有限オートマトン
$DFA=(Q,\Sigma,\delta,q_0,F)$
ここで、$Q$は状態集合、$\Sigma$はアルファベット、$\delta$は状態遷移関数、$q_0$は初期状態、$F$は受理状態集合。
$\delta: Q\times\Sigma\rightarrow Q$。
$L(M) = \{w|\hat\delta(q_0,w)\in F\}$は$M$の受理言語といい、または$M$の言語。
DFAの言語は正規言語といい。
DFAで、任意の状態は任意の入力への対処すべき。
2.2 非決定的有限オートマトン
$NFA=(Q,\Sigma,\delta,q_0,F)$
ここで、$Q$は状態集合、$\Sigma$はアルファベット、$\delta$は状態遷移関数、$q_0$は初期状態、$F$は受理状態集合。
$\delta: Q\times\Sigma\rightarrow 2^Q$。
$L(M) = \{w|\hat\delta(q_0,w)\cap F\neq\varnothing\}$は$M$の受理言語といい、または$M$の言語。
2.3 DFA $\leftrightarrow$ NFA
DFA、NFAは同じ言語表現能力を持つ——正規言語。
まず、DFAは特別なNFA。
NFAからDFAへの変換
- 初期状態集合からひとつずつ、NFAの状態集合をDFAの状態へ変換。
- DFA状態$\varnothing$を設置し、必要な状態遷移を添付。
2.4 ε動作付き非決定的有限オートマトン
$\varepsilon NFA=(Q,\Sigma,\delta,q_0,F)$
ここで、$Q$は状態集合、$\Sigma$はアルファベット、$\delta$は状態遷移関数、$q_0$は初期状態、$F$は受理状態集合。
ここで、$\delta: Q\times(\Sigma\cup\{\varepsilon\})\rightarrow 2^Q$。
$L(M) = \{w|\hat\delta(q_0,w)\cap F\neq\varnothing\}$は$M$の受理言語といい、または$M$の言語。
2.5 ε-NFAの構造テンプレート
2.5.1 最後の 3 文字のうち少なくとも一つ文字は「1」

2.5.2 最初の 3 文字のうち少なくとも一つ文字は「0」

2.6 DFA $\leftrightarrow$ ε-NFA
DFA、NFA、ε-NFAは同じ言語表現能力を持つ——正規言語。
2.6.1 ε閉包
ある状態の閉包とは、自体を含み、ε動作によって遷移できる状態の集合。
2.5.1のε閉包
$E(q_0)=\{q_0\}, E(q_1)=\{q_1,q_2,q_3\}$
$E(q_2)=\{q_2,q_3\}, E(q_3)=\{q_3\}$
2.6.2 ε-NFAからDFAへの変換
- 諸ε-NFA状態のε閉包を求め。
- 初期状態集合ε閉包からひとつずつ、ε-NFAの状態集合ε閉包をDFAの状態へ変換。
- DFA状態$\varnothing$を設置し、必要な状態遷移を添付。
2.7 小テスト
I.$\Sigma=\{0,1\}$, $L=\{w|01$は$w$の部分文字列$\}$,$L$を受理出来る一つDFAを求め。
II.$\Sigma=\{0,1\}$, $L=\{w|w$で、$1$が偶数回出現$\}$,$L$を受理出来る一つDFAを求め。
III.$\Sigma=\{0,1\}$, $L=\{w|w$で、$0,1$が偶数回出現$\}$,$L$を受理出来る一つDFAを求め。
IV.$\Sigma=\{0,1\}$, $L=\{w|010$は$w$の部分文字列$\}$,$L$を受理出来る一つDFAを求め。
V.$\Sigma=\{0,1\}$, $L=\{w|010$は$w$の部分文字列ではない$\}$,$L$を受理出来る一つDFAを求め。
VI.$\Sigma=\{0,1\}$, $L=\{w|w$で、$01$が奇数回出現$\}$,$L$を受理出来る一つDFAを求め。
VII.$\Sigma=\{0,1\}$, $L=\{w|w$で、$0,1$の出現回数が同$\land w $の全ての接頭部で、$0,1$の出現回数差の絶対値$\leq1\}$,$L$を受理出来る一つDFAを求め。
VIII.$\forall L(|L|<\aleph_0\rightarrow L$は正規言語$)$
IX. $\varnothing$, $\{\varepsilon\}$のDFAを求め。
X.$\Sigma=\{0,1\}$, $L=\{w||w|\geq 3\land w $の第2文字$\neq w$の第1文字$\}$,$L$を受理出来る一つNFAを求め。
XI.$\Sigma=\{a,b,c\}$, $L=\{w||w|\geq 1\land w $の最後3文字のうち少なくとも一つ文字は$c$でない$\}$,$L$を受理出来る一つNFAを求め。
XII.$\Sigma=\{a,b,c\}$, $L=\{w||w|\geq 2\land w $の2番目と4番目の文字の間で、少なくとも 一つ文字は$c$でない$\}$,$L$を受理出来る一つNFAを求め。
XIII.$\Sigma=\{a,b,c\}$, $L=\{w||w|\geq 4\land w $の最初の5文字には部分文字列$bac$が含まれ$\land$最後の5文字には部分文字列$acb$が含まれ$\}$,$L$を受理出来る一つNFAを求め。このNFAをDFAへ転換。
2.8 Answer
XIIIで、$q_{10}$を含む状態は全て受理状態。
2.9 検定問題
大菜之后上。
。
3. 正規表現
DFA、NFA、ε-NFAは同じ言語表現能力を持つ——正規言語。
2.6
正規表現は正規言語をより簡潔に表現できる。
3.1 概念
| 表記 | 意味 |
| $0$ | $\{0\}$ |
| $0^*$ | $\{\varepsilon,0,00,000,…\}$ |
| $0^+$ | $\{0,00,000,…\}$ |
| $01$ | $\{01\}$ |
| $0+1$ | $\{0,1\}$ |
| $10^+1^*$ | $\{10,101,1011,10111,…,100,1001,10011,…,1000,…\}$ |
| $(0,1)^*$ | $\{\varepsilon,0,1,00,01,10,11,000,…\}$ |
| $(1+\varepsilon)0+1$ | $\{10,0,1\}$ |
| $0\varnothing$ | $\varnothing$ |
| $0+\varnothing$ | $\{0\}$ |
単純な正規表現を書くのは簡単です。より複雑な正規表現は通常、有限オートマトンによって変換されます。
詳細については、この部分の小テストを参照してください。
3.2 有限オートマトンから正規表現へ
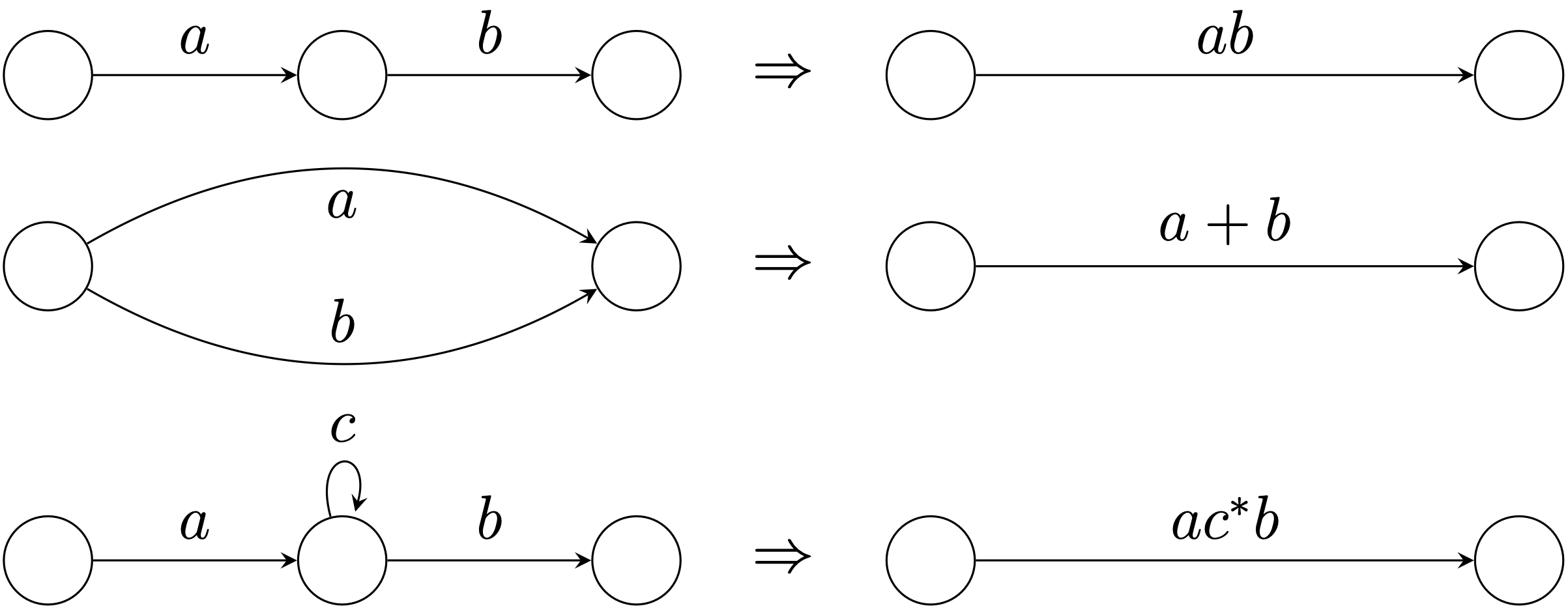
状態縮約法
3.2.1 原子縮約
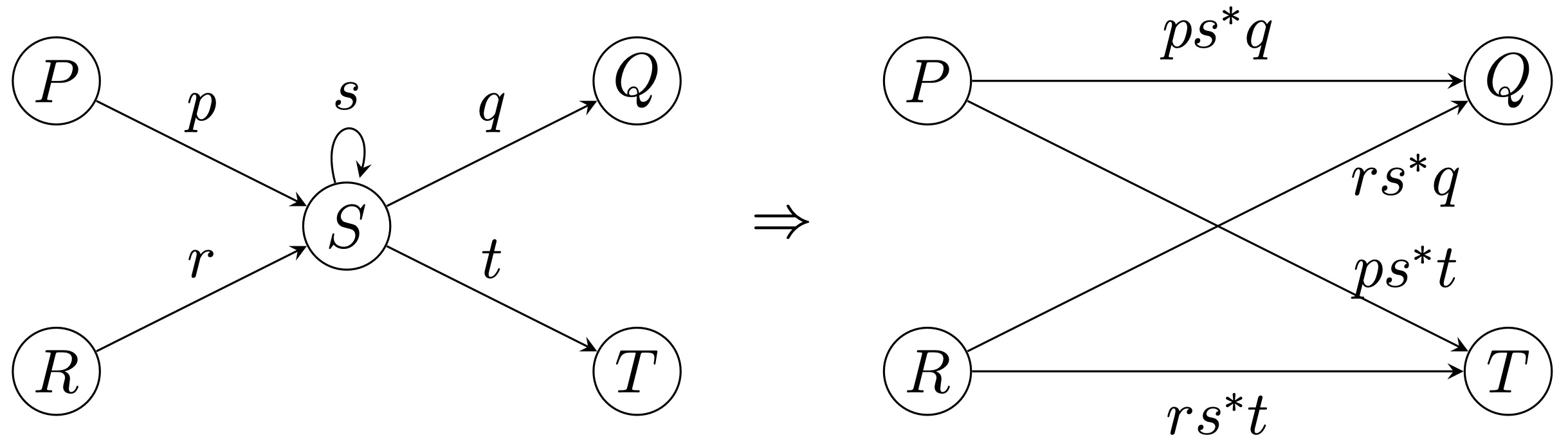
3.2.2 ネット縮約
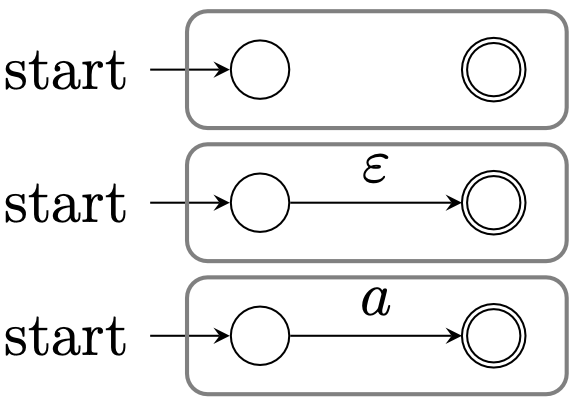
3.3 正規表現から有限オートマトンへ
3.3.1 原子構造
$a$は正規表現。
| $\varnothing$のFA |
| $\varepsilon$のFA |
| $a$のFA |
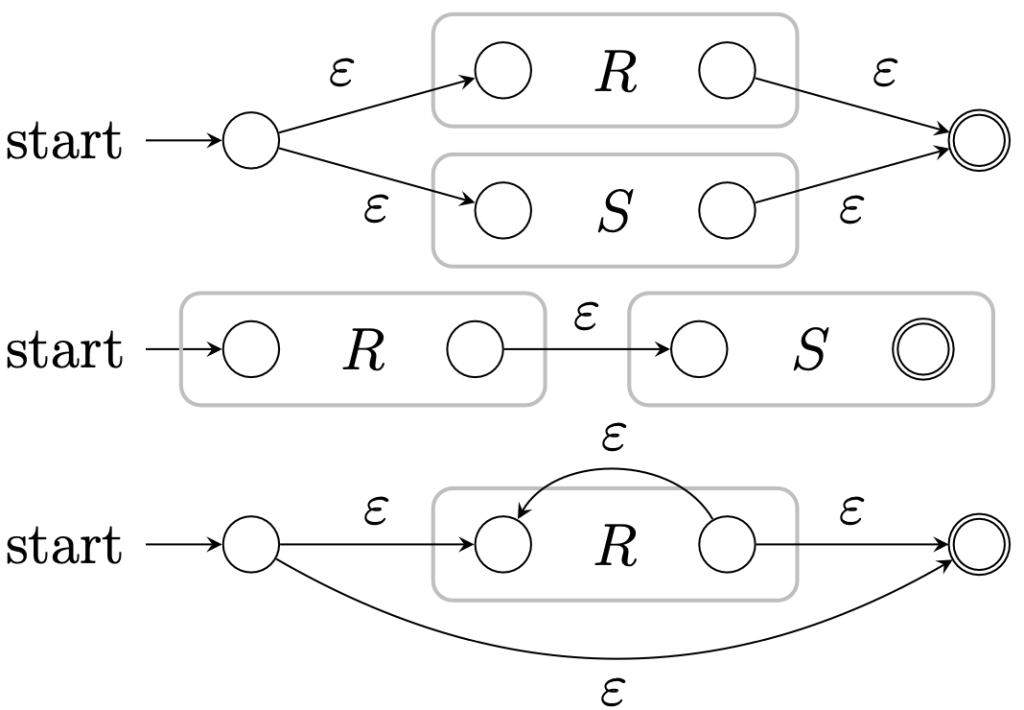
3.3.2 結合構造
$r$, $s$は正規表現。
$r+s$のFA |
$rs$のFA |
$r^*$のFA |
3.4 正規表現の性質
$R=(RE, +, \cdot)$は半環、$RE$は正規表現の全体。
$R$は以下の性質を持つ。($L,M,N$は正規表現)
3.4.1 代数系性質
- $L+M=M+L$
- $(L+M)+N=L+(M+N)$
- $(LM)N=L(MN)$
- $\varnothing+L=L+\varnothing=L$
- $\varepsilon L=L\varepsilon= L$
- $\varnothing L=L\varnothing=\varnothing$
- $L(M+N)=LM+LN$
- $(M+N)L=ML+NL$
- $LM\neq ML$(一般は)
- $L+L=L$
3.4.2 他の性質
- $(L^*)^*=L^*$
- $\varnothing^*=\varepsilon$
- $\varepsilon^*=\varepsilon$
- $L^*=L^++\varepsilon$
- $L^+=LL^*=L^*L$
- $L=\varepsilon+L$
- $(L+M)^*=(L^*M^*)^*$
- $L^*L^*=L^*$
3.4.3 構造的性質
3.4.3.1 反複補題
正規言語$R$に対して次の条件を満たす定数$N$が存在する。
$|w|\geq N$の$R$内の語$w$は次の条件を満たすように$w = xyz$と分解できる。
(1) $|xy| \leq N$
(2) $|y| \geq 1$または$y\neq\varepsilon$
(3) $\forall i \geq 0(xy^iz\in R)$
この定数$N$は、$R$を受理する最小(状態数が最も少ない)の有限オートマトンの状態数を越えない。
特に、有限言語の場合、反複補題も成立。
この補題は、正規言語ではないと判断するしかない。
つまり、反複補題の成立は言語正規性の成立を保証するものではない。
Myhill-Nerode則
$\Sigma$上の言語 $L$に対して定義される右不変な同値関係を$R_L$とするとき、以下の命題は互いに同等である。ここで、同値関係の指数とはその同値類の濃度 (集合の要素数)である。
(1)$L$は正規言語(有限オートマトンの受理集合)である。
(2)$L$は、有限指数を持つ右不変な同値関係$R_i$のその幾つかの同値類の直和として表される。
(3)同値関係 $R_L$の指数は有限である。
3.4.3.2 正規表現の結合
$L,R$は正規表現。なら次の形式も正規表現:
- $LR$
- $L\cup R$
- $L^*$
- $\bar L$
- $L\cap R$
- $\varphi(L)$, $\varphi:\Sigma\rightarrow\Gamma^*$は2つのアルファベットの(準同型)写像
- $\varphi^{-1}(R)$, $\varphi:\Sigma\rightarrow\Gamma^*$は2つのアルファベットの(逆準同型)写像
- $L^R$、ここの$R$はリバース
- $L-R$
DFAの構造方法
。。。。。。。。还没准备好图。。。。。。。
3.5 正規言語の判定問題
3.5.1 正規表現の空性、有限性
$n$つ状態を持つ有限オートマトン$M$の言語が空$\leftrightarrow$ $\forall w(w\in \Sigma^* \land |w|\leq n\rightarrow w\notin L(M))$
$n$つ状態を持つ有限オートマトン$M$の言語が無限集合$\leftrightarrow$ $\exists w(w\in \Sigma^* \land n\leq |w|\leq 2n\rightarrow w\in L(M))$
したがって、正規表現に対して:
受理集合が空かどうかを判断するアルゴリズムが存在し、それは長さが$n$未満の全ての文字列をチェックするでよい。
受理集合が無限かどうかを判断するアルゴリズムが存在し、それは長さが$n$から$2n−1$までの全ての文字列をチェックするでよい。
3.5.2 正規表現の同値性
有限オートマトン$M,N$に同値かどうかを判断するアルゴリズムが存在し。
$(\bar L(M)\cap L(N))\cup(L(M)\cap \bar L(N))$の空性を判断するでよい。
従って、正規表現の同値性を判断する方法もある。
3.6 DFAの最小化
同値状態:
(1)受理状態
(2)
(3)
3.7 小テスト
I.$(a+b)^*(a+bb)$は何。
II.$\Sigma=\{0,1\}$, $L=\{w||w|= 2\land w $の第2文字は$1\}$,$L$の一つ正規表現を求め。
III.$\Sigma=\{0,1\}$, $L=\{w|000$は$w$の部分文字列$\}$,$L$の一つ正規表現を求め。
IV.$\Sigma=\{0,1\}$, $L=\{w$の最後2文字は$01\}$,$L$の一つ正規表現を求め。
V.$\Sigma=\{0,1\}$, $L=\{w|w$の最初文字$=$の最後文字$\}$,$L$の一つ正規表現を求め。
VI.$\Sigma=\{0,1\}$, $L=\{w|w$で$0$の後に$1$, $1$の後に$0\}$,$L$の一つ正規表現を求め。
VII.$\Sigma=\{0,1\}$, $L=\{w|w$で$0$の後に$1$, $1$の後に$0\}$,$L$の一つ正規表現を求め。
VIII.$\Sigma=\{0,1\}$, $L=\{w$の後ろから5番目文字が$1\}$,$L$の一つ正規表現を求め。
IX.$\Sigma=\{0,1\}$, $L=\{w||w|\geq 1\land w $の最初5文字のうち少なくとも一つ文字は$1\}$,$L$の一つ正規表現を求め。
X.$\Sigma=\{0,1\}$, $L=\{w||w|\geq 1\land w $の最後5文字のうち少なくとも一つ文字は$1\}$,$L$の一つ正規表現を求め。
XI.$\Sigma=\{a,b,c\}$, $L=\{w|a,b$は$w$の文字$\}$,$L$の一つ正規表現を求め。
XII.$\Sigma=\{0,1\}$, $L=\{w|$全ての$00$は$11$の前で出現$\}$,$L$の一つ正規表現を求め。
XIII.$\Sigma=\{0,1\}$, $L=\{w=xy|x\in\Sigma^*\land y=y^R\land |y|=3$,$L$の一つ正規表現を求め。
XIV.$\Sigma=\{0,1\}$, $L=\{w|00,11$は$w$の部分文字列ではない$\}$,$L$の一つ正規表現を求め。
XV.$\Sigma=\{0,1\}$, $L=\{w=0^m1^n|m,n\geq 0\land 2\mid(m+n)$,$L$の一つ正規表現を求め。
XVI.$\Sigma=\{0,1\}$, $L=\{w|w$の最後文字は$1$なら$2\nmid|w|\land |w|\geq 1$,$L$の一つ正規表現を求め。
XVII.$\Sigma=\{0,1\}$, $L=\{w||w|\geq 2\land w $の最初の5文字には部分文字列$00$が含まれ,$L$の一つ正規表現を求め。
XVIII.$\Sigma=\{0,1\}$, $L=\{w||w|\geq 2\land w $の2番目と5番目の文字の間で、少なくとも一つ文字は$1\}$,$L$の一つ正規表現を求め。
XIX.$\Sigma=\{0,1\}$, $L=\{w|w$の後ろから5番目文字が$1,w$には、$1$が3つだけあります$\}$,$L$の一つ正規表現を求め。
XX.$(0+1)^*1(0+1)$のNFAを求め。
XXI.$L=\{0^n1^n\}$は正規言語でないを証明。
XXII.$L=\{w$で、$0,1$の出現回数が同$\}$は正規言語でないを証明。
XXIII.$L=\{0^i1^j|i>j\}$は正規言語でないを証明。
XXIV.$L=\{0^{n!}\}$は正規言語でないを証明。
XXV.$L=\{0^n(0+1)^*1^n)\}$は正規言語ですか。
XXVI.$\Sigma=\{0,1\}$, $L=\{w|w=w^R\}$,$L$は正規言語ですか。
3.8 Answer
3.9 検定問題
4. 文脈自由文法
4.1 概念
4.1.1 文脈自由文法
$G=(V,T,P,S)$
$V$は非終端記号集合、$T$は終端記号集合、$P$は生成規則集合、$S\in V$は開始記号。
$P$の元は生成規則といい。
4.1.2 文脈自由言語
$T^*$上の言語$L\subseteq T^∗$ に対して、$L$を生成する文脈自由文法$G$が存在するとき、$L$を文脈自由言語といい。
$L=\{w|w\in T^*\land S\Rightarrow w\}$
4.1.3 導出と帰結
ある生成規則$A\rightarrow \gamma$によって、
$\alpha A\beta\Rightarrow\alpha\gamma\beta$という操作を導出といい、
$\alpha A\beta\Leftarrow\alpha\gamma\beta$という操作を帰結といい。
4.1.4 最左導出と最右導出
最左導出:文字列の最左非終端記号のみを置き換える導出。
最右導出:文字列の最右非終端記号のみを置き換える導出。
最左導出、最右導出は一意存在的。
4.1.5 構文木
。。。。。
4.2 曖昧文法
文脈自由文法$G$で、ある語$w ∈ L(G)$に対して 2 つ以上導出木を持つ時、$G$は曖昧文法といい。
一部の曖昧文法は、文法再構築によって曖昧さを回避できる。ですが、文法再構築でも曖昧さを回避できない状況もある。この時は、この文脈自由文法は本質曖昧的といい、その言語を本質曖昧言語といい。
$L=\{a^ib^jc^k|i=j\lor j=k\}$は本質曖昧言語。
4.3 文法標準化
4.3.1 文法簡約化
4.3.1.1 無用記号の除去
生記号集合
$G_s=T\cup\{X|X\Rightarrow w\land w\in \Sigma^*\land X\in V\}$
到達可能記号
$R_s=\{S\}\cup\{X|X$は$\alpha$の文字$\land Y\rightarrow \alpha\in P \land Y\in R_s\}$
無用記号は
$U_s=V\cup T-G_s-R_s$
$P$で、$U_s$の元を含む生成規則を$P$から除去。
4.3.1.2 ε-生成規則の除去
。。。。。。
4.3.1.3 単位規則の除去
$A\rightarrow B, B\rightarrow w$なら$A\rightarrow w$を用いて簡約
4.3.2 文法標準形
4.3.2.1 チョムスキー標準形
$\varepsilon$なし文脈自由文法の生成規則は全て次のような形式へ変換できる。
$A\rightarrow BC, A\rightarrow a(A,B,C\in V, a\in T)$
4.3.2.2 グライバッハ標準形
文脈自由文法の生成規則は全て次のような形式へ変換できる。
$A\rightarrow a\alpha(A\in V, a\in T, \alpha\in V^*)$
特に$A\rightarrow A\alpha|\beta$は次の2式へ変換。
$A\rightarrow \beta B|\beta$
$B\rightarrow \alpha B|\alpha$
4.4 プッシュダウンオートマトン
4.4.1 基本概念
$PDA=(Q,\Sigma,\Gamma,\delta,q_0,Z_0,F)$
ここで、$Q$は状態集合、$\Sigma$はアルファベット、$\Gamma$はスタックアルファベット、$\delta$は状態遷移関数、$q_0$は初期状態、$Z_0$スタック末端記号、$F$は受理状態集合。
$\delta: Q\times(\Sigma\cup\{\varepsilon\})\times\Gamma\rightarrow 2^{Q\times\Gamma^*}$。
状態遷移表記$p,X/\alpha$は、
$p$を入力のとき、今のスタック頂端記号は$X$、この$X$をポップアウト、$\alpha$の文字を一つずつスタックへプッシュ。
即座解釈
(今の状態、まだ受けられない文字列、スタック状況)
即座解釈の状態遷移
例:$\{q_3,abbac,XZYZ_0\} \vdash\{q_4,bbac,YYZYZ_0\}$
4.4.2 プッシュダウンオートマトンの受理言語
$L(P) = \{w|(q_0,w,Z_0)\vdash^*(p,\varepsilon,\alpha)\land p\in F\}$は$P$の状態受理言語といい。
$N(P) = \{w|(q_0,w,Z_0)\vdash^*(p,\varepsilon,\varepsilon)\}$は$P$のスタック受理言語といい。
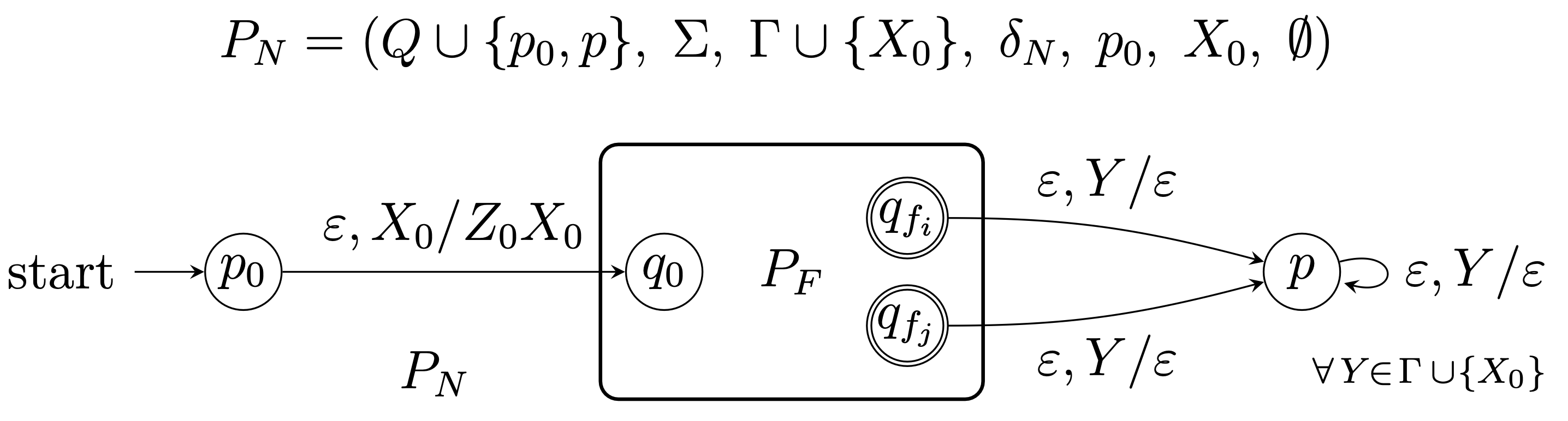
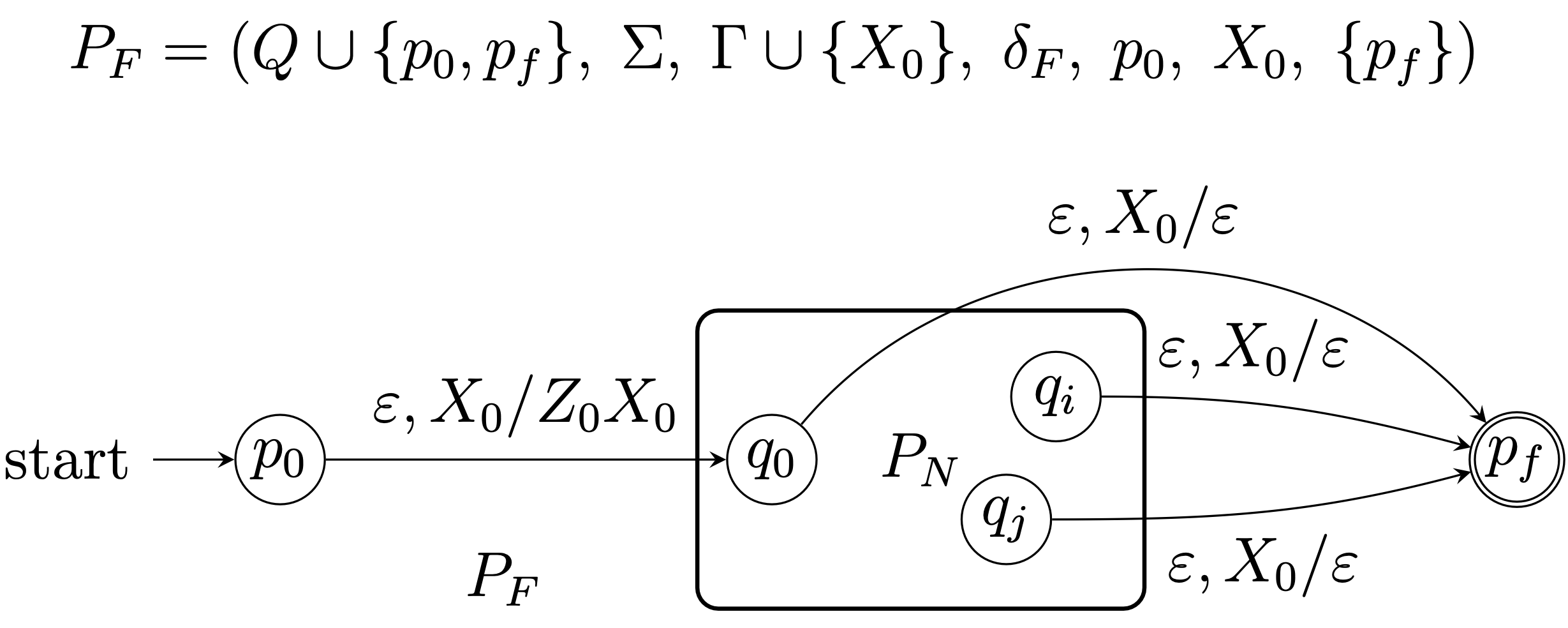
$P_N$(スタック受理)$\Leftrightarrow P_F$(状態受理)の方法
$P_F\rightarrow P_N$
$P_N\rightarrow P_F$
4.4.3 CFGからPDAへ
- PDAの構造はスタック受理的$start\rightarrow\LARGE\circ\small q_0$
- 全ての生成規則$A\rightarrow \alpha$に、$q_0$で状態遷移規則$\varepsilon,A/\alpha$をつけて
- 全ての終端記号$t\in T$に、$q_0$で状態遷移規則$t,t/\varepsilon$をつけて
特に、もしCFGはグライバッハ標準形、なら全ての生成規則$A\rightarrow a\alpha$に、$q_0$で状態遷移規則$a,A/\alpha$をつけてでいい。
4.4.4 PDAからCFGへ
$P=(Q,\Sigma,\Gamma,\delta,q_0,Z_0,F)$の文脈自由文法$G=(V,T,P,S)$を求め
生成規則集合$P$で、
- (1) $\forall p\in Q$に対して、$|Q|$つの生成規則$S\rightarrow [q_0Z_0p]$を添付。
- (2) $\forall (p,Y_1Y_2\cdots Y_n)\in \delta(q,a,X)$に対して、$|Q|^n$つの生成規則$[qXr_n]\rightarrow a[pY_1r_1][r_1Y_2r_2] · · · [𝑟_{𝑛−1}Y_nr_n]$を添付。
$a\in\Sigma\cup\{\varepsilon\}, X,Y_i\in\Gamma, r_i$は$Q$内の任意状態。
$Y_1Y_2\cdots Y_n=\varepsilon$とすると、生成規則は$[qXp]\rightarrow a$。
4.5 決定的プッシュダウンオートマトン
4.5.1 基本概念
$PDA=(Q,\Sigma,\Gamma,\delta,q_0,Z_0,F)$に、次の2条件を満足ならこれを決定的プッシュダウンオートマトンといい。
$\forall a(a\in\Sigma\cup\{\varepsilon\} \rightarrow |\delta(p,a,X)|\leq1)$
$\forall a(a\in\Sigma\land|\delta(p,a,X)|=1\rightarrow\delta(p,\varepsilon,X)=\varnothing)$
4.5.2 PDAとの区別
DPDAは$\{ww^R\}$を受理出来ない。
4.5.3 DPDAの受理言語
語頭属性を満たすとは、任意の語が他のいかなる語の接頭部になっていないという属性である。
あるDPDAのスタック受理言語は$L \Leftrightarrow L$は語頭属性を満たす。
DPDAの状態受理言語は決定的文脈自由文法といい。
DPDAの受理言語の文法は本質曖昧文法ではない。
本質曖昧でない言語はDPDAによって識別と限らない。
スタック受理$DPDA\subset$状態受理$DPDA\subset PDA\subset LBA\subset TM$
4.6 文脈自由言語の構造的性質
4.6.1 反複補題
文脈自由言語$L$に対して次の条件を満たす定数$N$が存在する。
$|z|\geq N$の$L$内の語$z$は次の条件を満たすように$z = uvwxy$と分解できる。
(1) $|vwx| \leq N$,
(2) $|vx| \geq 1$または$vx\neq\varepsilon$,
(3) $\forall i \geq 0 (uv^iwx^iy\in L)$.
4.6.2 文脈自由言語の結合
$L,R$は文脈自由言語。
其々の文法は$G_L=\{V_L,T_L,P_L,S_L\}$,$G_R=\{V_R,T_R,P_R,S_R\}$
なら次の形式も文脈自由言語:
- $LR$
$G_{LR}=\{V_L\cup V_R\cup\{S\}, T_L\cup T_R, P_L\cup P_R\cup\{S\rightarrow S_LS_R\}, S\}$ - $L\cup R$
$G_{L\cup R}=\{V_L\cup V_R\cup\{S\}, T_L\cup T_R, P_L\cup P_R\cup\{S\rightarrow S_L|S_R\}, S\}$ - $L^*$
$G_{L^*}=\{V_L\cup\{S\}, T_L, P_L\cup\{S\rightarrow S_LS|\epsilon\}, S\}$ - $\varphi(L)$, $\varphi:\Sigma\rightarrow\Gamma^*$は2つのアルファベットの(準同型)写像
- $\varphi^{-1}(R)$, $\varphi:\Sigma\rightarrow\Gamma^*$は2つのアルファベットの(逆準同型)写像
- $L^R$、ここの$R$はリバース
$G_{L^R}=\{V_L,T_L,\{A\rightarrow\alpha^R|A\rightarrow\alpha\in P_L\},S_L\}$ - $\tau(L)$, $\tau : \Sigma\rightarrow2^{\Gamma^*}$は代換といい。
代換は「$\Sigma$の文字を$\Gamma$でのある言語へ写像」。
次の形式は文脈自由言語でないも可能。
- $L\cap R$
- $\bar L$
ただし、もし$R$は正規言語、なら$L\cap R$は文脈自由言語。
ここは、1つの状態受理PDAはLを実現、DFAはRを実現。2つのオートマトンが同時受理でいい。
$PDA_{L}=(Q_P,\Sigma,\Gamma,\delta_P,q_P,Z_0,F_P)$
$DFA_{R}=(Q_D,\Sigma,\delta_D,q_D,F_D)$
$PDA_{L\cap R}=(Q_P\times Q_D, \Sigma,\Gamma,\delta,[q_p,q_d],Z_0,F_P\times F_D)$
$\delta([p,q],\varepsilon,X)=\{([p,s],\beta)|(s,\beta)\in\delta_P(q,\varepsilon,X)\}$
$\delta([p,q],a,X)=\{([r,s],\beta)|r=\delta_D(p,a)\land(s,\beta)\in\delta_P(q,a,X)\}(a\in\Sigma)$
4.6 文脈自由言語の判定問題
4.6.1 文脈自由言語の判定可能問題
$S$が生記号ならこの文脈自由言語は空じゃない。
CYKアルゴリズムはある語$w$が$L(G)$内にあるかどうかを判断する、特に$G$は既にチョムスキー標準形化。
4.6.2 文脈自由言語の判定不可能問題
次のものは、論理的判断不可能となります。
- ある文脈自由文法$G$は曖昧文法かどうかを判断する。
- ある文脈自由言語$L$は本質曖昧言語かどうかを判断する。
- 文脈自由言語のかつが空かどうかを判断する。
- 2つの文脈自由文法・言語が同じかどうかを判断する。
- 文脈自由言語の補言語が空かどうかを判断する。
- ある文脈自由言語$=\Sigma^*$を判断する。
4.7 小テスト
I. $L=\{a^mb^n|m\geq 0\land 2m\leq n\leq3m\}$の一つ文脈自由文法を求め。
II.$L=\{w|w\in(0+1)^*\land 0,1$の出現回数が同$\}$の一つ文脈自由文法を求め。
III.$L=\{w|w\in(0+1)^*\land 0,1$の出現回数差の絶対値$= 2\}$の一つ文脈自由文法を求め。
IV.$L=\{w|w\in(0+1)^*\land 0,1$の出現回数が不同$\}$の一つ文脈自由文法を求め。
V.$L=\{0^n1^n|n\geq 1\}$の一つプッシュダウンオートマトンを求め。
VI.$\Sigma=\{0,1\}$, $L=\{ww^R|w\in\Sigma^*\}$の一つプッシュダウンオートマトンを求め。
VII.$L=\{w$で、$0,1$の出現回数が同$\}$の一つプッシュダウンオートマトンを求め。
VIII.$L=\{w$で、$0,1$の出現回数が同じじゃない$\}$の一つプッシュダウンオートマトンを求め。
IX.$\Sigma=\{0,1\}$, $L=\{w|w $の全ての接頭部で、$a$の出現回数は$b$の出現回数の2倍より大$\}$の一つプッシュダウンオートマトンを求め。
X.$L=\{0^n1^m|0\leq n\leq m\leq2n\}$の一つプッシュダウンオートマトンを求め。
XI.$\Sigma=\{a,b,c\}$, $L=\{a^mb^nc^k|a+2m=k\}$の一つプッシュダウンオートマトンを求め。
XII.$L=\{0^n1^{n+2}\}$の一つ決定的プッシュダウンオートマトンを求め。
XIII.$L=\{0^n1^n2^n\}$は文脈自由言語でないを証明。
XIV.$L=\{0^n1^{n^2}\}$は文脈自由言語でないを証明。
XV.$\Sigma=\{0,1\}$,$L=\{ww|w\in\Sigma^*\}$は文脈自由言語でないを証明。
XVI.$\Sigma=\{a,b\}$, $L=\{w|w$で$0,1$の出現回数が同$\}$, 代换$s(a)=L_a= {0^n 1^n | n \geq 1}$
$s(b)=L_b= {ww^R | w\in(0+1)^*}$
$s(L)$の一つ文脈自由文法を求め。
4.8 Answer
4.9 検定問題
5. Turing マシーン
5.1 標準 Turing マシーン
$TM$は有限内部状態$Q$を有し、入力文字列を載せたマス目に区切られた片側(また両側無限)テープをヘッドを記号を読み、内部状態に応じてテープ記号を書き換えヘッドを左右に移動させながら動作を繰り返す。最初に与えた入力文字列の以外のテープのマス目は空白記号で埋められている。
5.1.1 基本概念
$TM=(Q,\Sigma,\Gamma,\delta,q_0,B,F)$
ここで、$Q$は状態集合、$\Sigma$はアルファベット、$\Gamma$はテープアルファベット、$\delta$は状態遷移関数、$q_0$は初期状態、$B$ブランク記号、$F$は受理状態集合。入力はすでに左右無限長テープに書かれた。ヘッドの初期位置は第一入力記号の上。
$\delta: Q\times\Gamma\rightarrow Q\times\Gamma\times\{L,R\}$。
状態遷移表記$X/Y,L$は、
ヘッドがテープ記号$X$を読むと、テープ記号$X$を$Y$に書き換えてヘッドを左に移動する。
即座解釈
$X_1,X_2,\cdots,X_{i-1},pX_i,X_{i+1}\cdots,X_n$
ヘッドはいつも状態の右側にあり。
即座解釈の状態遷移
例:$X_1,X_2,\cdots,X_{i-1},pX_i,X_{i+1}\cdots,X_n$ $\vdash$ $X_1,X_2,\cdots,X_{i-1},X_i,qX_{i+1}\cdots,X_n$
5.1.2 入力受理
受理状態に達しないとき、TM は動作を停止する。この時、入力は受理されない。
受理状態に達したとき、TM は入力を受理して計算を停止したという。
TM が入力を受理しないときは、かならずしも停止するわけではない。(これは論理的判断不可能問題)
5.1.3 Turing マシーンの言語
あるTuring マシーンの言語は帰納的可算言語といい。
特に、どんな入力でもあるTMの動作を停止させる言語は帰納言語、あるいは決定可能といい。
5.2 他の Turing マシーン
5.2.1 Multi-track式
ヘッドは一度に複数の文字を読み取る、書き込むことができます。
5.2.2 Multi-tape式
複数のヘッドあり。
5.2.3 非決定的
DFAとNFAの関係に似てる。
5.2.4 テープが半無限的
テープが左無限長、または右無限長。
5.2.4 複数スタックPDA
複数のスタックを持つPDA。
5.3 Turing マシーンの表現能力
5.2の様々なオートマトンは、5.1の Turing マシーンと同値。
表現能力は帰納的可算言語。
5.4 小テスト
I.$L=\{0^n1^n|n\geq 1\}$の一つ Turing マシーンを求め。
II.$L=\{0^n1^n2^n|n\geq 1\}$の一つ Turing マシーンを求め。
III.$L=\{w$で、$0,1$の出現回数が同$\}$の一つ Turing マシーンを求め。
IV.『2進数+1』の Turing マシーンを求め。(例:$BBp\$1111BB\vdash BBq\$10000BB$)
IV.『正減算』の Turing マシーンを求め。(例:
$BBp00001000BB\vdash BBq0BB$ (4-3=1),
$BBp001000BB\vdash BBqBB$ (2-3=0))
IV.$\Sigma=\{a,b\}$, $L=\{wcw|w\in\Sigma^*\}$の一つ2 track 式 Turing マシーンを求め。
IV.$L=\{a^nb^nc^n|n\geq0\}$の一つ2スタックPDAを求め。
IV.$L=\{a^nb^nc^nd^ne^n|n\geq0\}$の一つ2スタックPDAを求め。

コメント
コメント一覧 (1件)
いいよ